平衡二叉树（AVL树）的实现

发表于 更新于 分类于

复习一下平衡二叉树，经常混以为就是最优二叉树，其实是最优二叉树是哈夫曼树，这个以后有机会再说。

平衡二叉搜索树（Self-balancing binary search tree）又被称为AVL树（有别于AVL算法），且具有以下性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树,它须保证树的深度是O(log N)。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 最小二叉平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列，可以参考Fibonacci(斐波那契)数列，1是根节点，F(n-1)是左子树的节点数量，F(n-2)是右子树的节点数量。

  这里主要思考的是二叉树的插入节点。查询节点和修改节点的操作都可以以时间O(logN)的复杂度执行，假如删除使用惰删除的话，那么时间也是O(logN)。所谓惰删除就是当删除一个节点时，并不是真正的进行了物理删除，只是设置了一个字段来标记这个节点是否被删除。使用惰删除是有很多好处的，物理删除可能将会像插入节点一样需要进行旋转，当然也可能不需要。但如过后期又想添加之前删除的节点，那么又只能重新插入节点，很大几率要进行旋转操作。如果使用惰删除，那么时间复杂度将大大降低，但是相应的会使用额外的存储空间。

  如果插入一个节点将导致一个树的不平衡，那么会有一个必须重新平衡的节点叫做α。由于任意节点最多有两个孩子，因此高度不平衡时，α两棵子树的高度差为2，这种不平衡可能会出现以下四种情况：

1.对α的左儿子的左子树进行一次插入。
2.对α的左儿子的右子树进行一次插入。
3.对α的右儿子的左子树进行一次插入。
4.对α的右儿子的右子树进行一次插入。

  情况1和4是对称的，情况2和3是对称的，所以实际上只有两种情况，但是编程还是要写四种情况。
  情况1和4是插入发生在“外边”的情况，左-左，右-右，这种情况通过一次单选转就可以完成调整，剩下两种情况是插入发生在“内部”的情况，左-右，右-左，这种情况需要进行双旋转来进行调整。

插入原理

单旋转

1526922814609.png

  上图是左单旋转，对k2的左儿子k1的左子树进行的一次插入，X、Y、Z分别表示表示k1、k2的儿子，可以看见X明显比Y和Z深，且比Z深2层。为恢复平衡，就应该把X上移一层，Z下移一层，这样就变成了上图中旋转后的样子，k2变成了k1的右孩子，Y变成了k2的左孩子，X和Z不变。

1526922837456.png

  右旋转类似，对k1的右孩子k2的右孩子进行了一次插入，导致Z的深度比X大2，同样是把X下移一层，Z上移一层，k1就变成了k2的左孩子，Y变成了k1的右孩子。

  个人是这样记忆的，如何找到哪个是k1哪个是k2呢？k1和k2必定有一个是不平衡的，先找到这两个节点，然后不管是左还是右旋转，都让k1小于k2，也就是大的节点是k2，小的节点是k1，k1、k2互换高度，一个上移，一个下移。

双旋转

但是单旋转无法解决另外两种情况

1526922852593.png

1526922863305.png

  我们要把Y看成是一个根和两棵子树，B和C中有一个比D深两层（除非它们都是空的），我们不能确定是哪一棵，也不需要确定是哪一棵，上图中画的时候B和C全部画的比D低一层半。整颗子树，我们看成四棵子树A、B、C、D和三个节点！k1、k2、k3。
  为了重新平衡，我们不能让k3继续当根节点，k1页不行，唯一的选择就是k2当做新的根。k1、k3分别作为k2的左右孩子，巧妙的是，A、B、C、D四棵子树依旧是按顺序排列过去的。

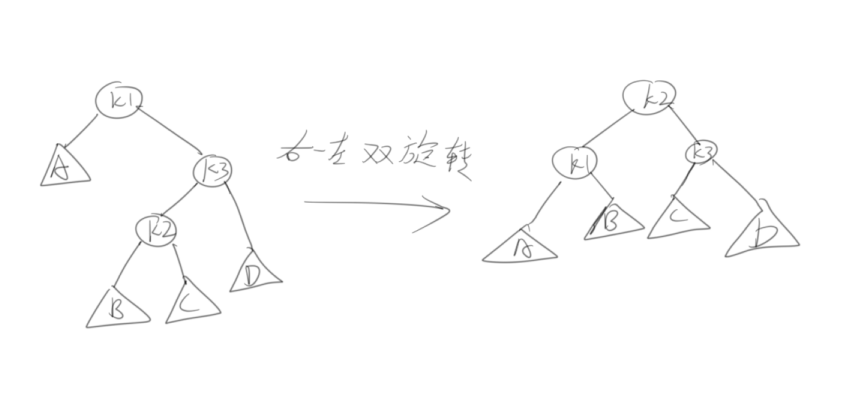
1526922873902.png

右-左双旋转如上，基本差不多。

总结下，遇到双旋转，先找到k1、k2、k3，三个节点最小的是k1，最大的是k2，旋转后，k1是k2左孩子，k3是k2右孩子，A、B、C、D依旧是原顺序排列。

对于插入，最多只需要一次旋转（如果双旋转也只视作一次旋转）

删除原理

AVL树的删除和BST的删除较为类似，首先找到需要删除的节点，找到之后，分为三种情况进行删除。

  • 需要删除的节点D是叶子节点，这种情况最简单，删除D之后，判断父节点DP是否需要调整，调整完成之后再调整DPP，DPPP，直到回溯到根节点。
  • 需要删除的节点D有一个孩子，将D的值改为孩子的值，然后删除叶子节点，这样就把情况转换成第一种情况了。
  • 需要删除的节点D有两个孩子，将D的值改为前驱或者后继的值，然后删除前驱或者后继的值，这样也就把情况装换成第一种情况了。

由此可见，我们只要重点讨论第一种情况就可以了，具体的删除流程如下：

  1. 删除节点D
  2. 判断删除节点的父节点DP是否满足AVL树的性质，如果不满足，则根据DP的状态进行旋转调整，并重新计算DP的高度，旋转分为四种情况，这里就不再细说。
  3. 继续向上调整DPP，检查DPP的平衡是否遭到破坏，之后再继续向上调整DPP，直到调整到根节点为止（即不断执行第三步）。实际上这里可以进行优化，在调整过程中如果经过某一次的调整，树的高度没有发生变化，那么就不必向上回溯调整了。

如何判断是否需要向上回溯调整呢？根据平衡因子。
  如果删除一个节点后，平衡因子为1/-1，说明高度未发生变化，那么就不需要向上调整了；如果删除一个节点后，因子变成0，说明树高度一定发生了变化，那么就需要向上回溯调整。如果平衡因子为2/-2，说明需要调整这棵树需要调整。

这里可以看到AVL树的可视化。

代码实现

  将一个新节点，插入到AVL树中去，递归的插入到相应的子树中后，如果树的高度不变，那么插入完成，如果出现了高度不平衡，那么我们将做适当的双旋转或者单旋转，并更新这些高度。另外一个问题就是二叉树的高度信息的存储，由于真正需要的是实际是子树高度的差，并且它一般很小，（1,0，-1等）

java的完整实现 点这里

下面给出的是C的代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class AvlNode {
public:
    AvlNode *left;
    AvlNode *right;
    int val;
    int height;        //这个节点的高度

    AvlNode() {
        left = NULL;
        right = NULL;
        val = -9999;
        height = 0;
    }
    AvlNode(int v) {
        left = NULL;
        right = NULL;
        val = v;
        height = 0;
    }

};
1
2
3
4
5
6
7
8
/*返回某个节点的高度*/
static int Height(AvlNode* node)
{
    if (node == NULL)
        return 0;
    else
        return node->height;
}
1
2
3
4
5
6
7
8
9
10
11
12
/*左单旋转*/
static AvlNode* SingleRotateWithLeft(AvlNode *k2)
{
    AvlNode *k1 = k2->left;
    k2->left = k1->right;
    k1->right = k2;

    k2->height = max(Height(k2->left), Height(k2->right)) + 1;
    k1->height = max(Height(k1->left), k2->height) + 1;

    return k1;
}
1
2
3
4
5
6
7
8
9
10
11
12
/*右单旋转*/
static AvlNode* SingleRotateWithRight(AvlNode *k1)
{
    AvlNode *k2 = k1->right;
    k1->right = k2->left;
    k2->left = k1;

    k1->height = max(Height(k1->left), Height(k1->right)) + 1;
    k2->height = max(k1->height, Height(k2->right)) + 1;

    return k2;
}
1
2
3
4
5
6
7
8
9
/*左-右双旋转*/
static AvlNode* DoubleRotateWithLeft(AvlNode *k3)
{
    /*k1,k2先右单旋转*/
    k3->left = SingleRotateWithRight(k3->left);

    /*k3,k2再左单旋转*/
    return SingleRotateWithLeft(k3);
}
1
2
3
4
5
6
7
8
9
/*右-左双旋转*/
static AvlNode* DoubleRotateWithRight(AvlNode *k1)
{
    /*k3,k2先左单旋转*/
    k1->right= SingleRotateWithLeft(k1->right);

    /*k1,k2再右单旋转*/
    return SingleRotateWithRight(k1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/*
向AVL树种插入节点
*/
AvlNode* insert(int val, AvlNode *T)
{
    if (T == NULL)
    {
        T = new AvlNode(val);
    }
    /*向左孩子插入*/
    else if (val < T->val)
    {
        T->left = insert(val, T->left);
        if (Height(T->left) - Height(T->right) == 2)
        {
            if (val < T->left->val)
                T = SingleRotateWithLeft(T);
            else
                T = DoubleRotateWithLeft(T);

        }
    }
    /*向右孩子插入*/
    else if (val > T->val)
    {
        T->right = insert(val, T->right);
        if (Height(T->right) - Height(T->left) == 2)
        {
            if (val > T->right->val)
                T = SingleRotateWithRight(T);
            else
                T = DoubleRotateWithRight(T);
        }
    }

    /*计算这个节点新的高度*/
    T->height = max(Height(T->left), Height(T->right)) + 1;
    return T;

}