红黑树（Red Black Tree）的实现

发表于 2018-06-01 更新于 2024-11-12 分类于数据结构与算法

红黑树（red black tree）是AVL树的一个变种，如果还不是十分了解AVL树，建议先读一下之前写的平衡二叉树的文章。平衡二叉树（AVL树）的实现

红黑树是具有下列着色性质的二叉查找树：
1.每一个节点或者着成红色，或者着成黑色；
2.根是黑色的；
3.如果一个节点是红色的，那么它的子节点必须是黑色的；
4.从一个节点到一个NULL指针的每一条路径必须包含相同数目的黑色节点。

图一所示便是一棵符合规范的红黑树。一般的来说，还有第五个性质。每个叶子节点（空节点）是黑色的。一开始看到这些性质的时候想到的是为什么要给树着色，有什么意义？其实红黑树和AVL树都是通过某种约束来维持着二叉树的平衡，AVL树规定每个节点的左右孩子的高度差不能大于1，从而保证了树的平衡。而红黑树通过颜色的约束来维持着二叉树的平衡，红黑树的这几条性质保证了从根到叶子最长的可能路径不多于最短的可能路径的两倍长，这棵树是大致平衡的。那么这两种平衡方法（也就是两种树）各有什么优缺点呢？红黑树牺牲了AVL树的严格高度平衡的优越条件，它的高度一般是比AVL树高的，所以在大量数据情况下，查询没有AVL树快。但是红黑树执行插入或删除的开销比较低，旋转的次数比较少，这一点是优势。因此总体来说，两者性能不会差多少，不同的场景选择不同的结构。

自底向上插入的过程

和之前写的AVL树、B-树一样，数据的插入都是一个难点。通常把新的节点作为树叶放在树中。如果我们把该节点涂成黑色，那么肯定不会满足条件4，因为建立了一条更长的黑节点的路径，因此新增节点必须涂成红色，我们尽量满足条件，以后的调整也就更简单些。如果父节点是黑色的，那么插入直接完成，不需要调整。如果父节点是红色的，我们新增节点也是红色的，将不满足第三个条件。在这种情况下，我们必须调整该树以确保条件3满足（且又不引起条件4被破坏）。完成调整这项任务的基本操作是颜色的改变和树的旋转。

图二是对图一插入25的结果，父节点为黑色，无冲突，不需要调整。

在继续讲解之前，必须要确认一下各节点的叫法

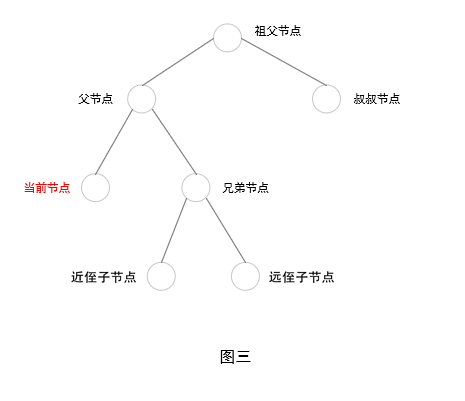
以下是两种冲突情况

1.红父红叔

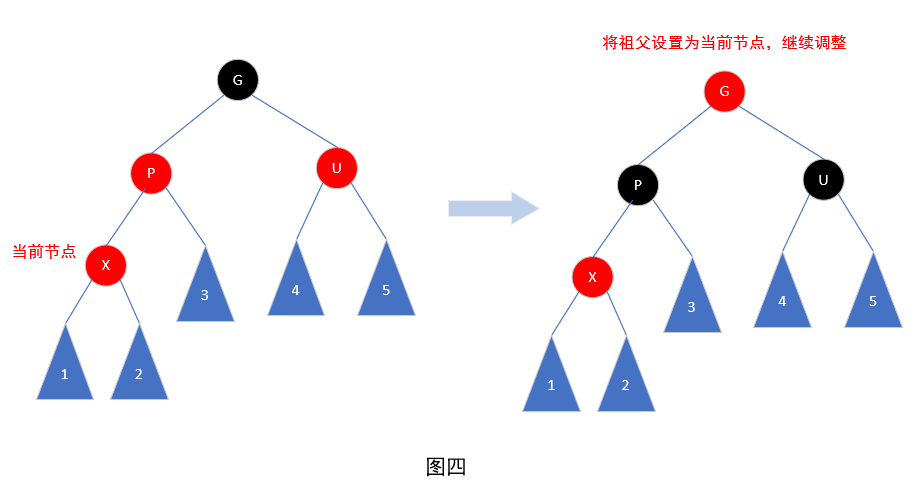
对于这种情况比较简单，不管当前节点是父节点的左孩子还是右孩子，也不需要管父节点是祖父节点的左孩子还是右孩子，只需要将父节点和叔叔节点都变成黑色，同时把祖父变成红色就可以了，最后将祖父节点设置为当前节点继续调整。因为这种情况不需要旋转，所以四种情况都是一样的处理方法，图四只列举了一张情况。

有一种特殊情况，如图四调整后的就是我们的红黑树，也就是说G是根节点，那么此时的调整方法是将G染成黑色即可。

我们对图二插入54的结果如下，当前节点由54变为了50。

2.红父黑叔

这种冲突的原因是违反了条件四，红节点下面出现了红节点，而非黑节点数量不同。这种情况还可以接续分为四种，但实际上只需要讨论两种，还有两个是镜像对称的。图7就是图6的两种对称情况。

这些情况不会发生在叶子节点（也就是插入新节点的第一次冲突）。原因很简单，以图6的第一张图作说明。假如发生在了叶子节点，那么在还没有插入X的时候，P肯定是叶子节点，并且P是红色的，而U是黑色的，那么G的左边的路径只有一个黑色节点（只能是空的叶子结点），而G的右边路径至少有两个黑色节点，黑色节点数不可能相同了，它不是一颗红黑树，都不是一颗红黑树，我们怎么插入节点？在插入新节点之前，我们肯定是会保证它是一颗符合规范的红黑树的。

要记住，我们是自底向上插入，自底向上调整，当前节点上面的部分一定是符合规范的。

认真观察图六图七，可以发现这种处突处理的方法也是旋转，如果你熟悉AVL树或者读过了我开头放的文章链接，那么相信你一定能看出来，第一种情况是使用的单旋转，第二种情况是双旋转，然后多了重新着色的过程。完成后，将祖父节点设置为当前节点，继续回溯调整。

剩下两种镜像情况

现在对图五的红黑树进行再次调整，调整结果见图八，图中已经标注了X、P、G、U，不理解的再看看上面两张图。其余情况不再举例了。

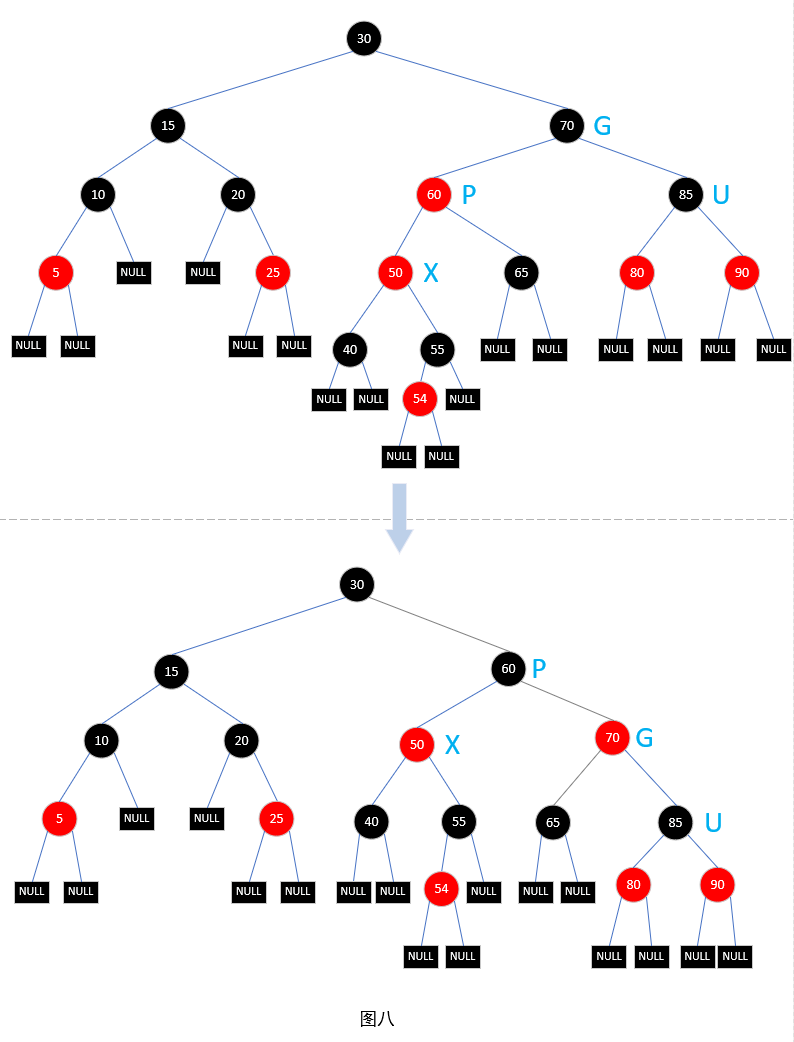
红黑树的插入操作不是很复杂，这里强烈建议你自己写一些数字然后按照上面的插入过程一个个走一遍，这样印象会非常深刻，也能更加深入的了解这个过程，你一定会感叹，红黑树真是巧妙。例如：10，5，6，16，1，11，12，21，15，17，14 按顺序插入的最终结果如图九所示。

自底向上删除的过程

相比于插入操作，红黑树的删除操作就比较麻烦了。

总体上来看分为两大步

第一步，将红黑树当一棵普通的二叉查找树，将节点删除

case 1：被删除的节点是叶子节点，直接删除节点。
case 2：被删除的节点只有一个孩子，不管是左孩子还是右孩子，删掉节点后，用孩子代替删除的节点
case 3：被删除的节点有两个孩子，先查找到这个节点的后继节点，（比它大的最小节点），用后继节点的值替代想要删除节点的值（想要删除的节点颜色不需要改变），然后删除掉后继节点。这样又巧妙地将问题转化为删除后继节点的情况了。因为删除后继节点，一共只有两种情况，要么为叶子节点，要么为只有一个有孩子的节点，不可能出现其它情况。这两种情况也就是case 1和case 2。

第二步，通过旋转和染色等一系列操作，使之重新成为一棵红黑树

下面开始详细分析。由第一步，不难明白，其实只要讨论删除的节点是叶子节点或只有一个孩子就可以。

case 2 比较简单，只有一种情况，当然要是细分的话，也可以分为两种镜像情况。这种情况是想要删除的节点为黑色，而且唯一的孩子是红色，当然，孩子的位置是无所谓的。为什么唯一的孩子是红色呢，因为如果是黑色，肯定会违反性质4。那为什么想要删除的节点不能为红色呢？那么我们假设想要删除的节点为红色，当然它也只有一个孩子，假如这个孩子是红色的，不管是左孩子还是右孩子，肯定都违反了红节点不能有红色儿子的要求（性质3）。假如这个孩子是黑色的，不管是左孩子还是右孩子，肯定违反了性质4。所以想要删除的节点不可能是红色。调整方法，简单明了，孩子替换父亲，并且染成黑色即可。见图十,D是我们想要删除的节点，P代表它的父节点，没有颜色说明什么颜色都可以，和D垂直，说明D是P的左孩子还是右孩子没有关系。

case 1 分为两大类，第一类，叶子节点是红色，直接删除，结束（见图十一）。额？这也算一个大类，其实是因为下一类情况特别麻烦

第二类，想要删除的叶子节点是黑色。这个可就要分为好多种情况了。

情况1 兄弟节点为黑色，且远侄子节点为红色。见图十二，没有上色说明什么颜色都可以。SL无论黑色红色都属于这种情况。（注意：如果SL是黑色的话，那么它一定是空节点NULL；如果SL是红色的话，那么它肯定和SR一模一样，只有有两个黑色的NULL节点）

对于这种情况，删除掉D后，有一边会少了一个黑色节点，但有一个侄子是红色的，那么我们可以通过旋转和染色重新完成平衡，这个过程在P的内部就可以解决，所以和P的颜色无关。调整过程为将P和S的颜色互换，然后进行一次右旋，最后将SR染成黑色即可。（以第一种情况说明）

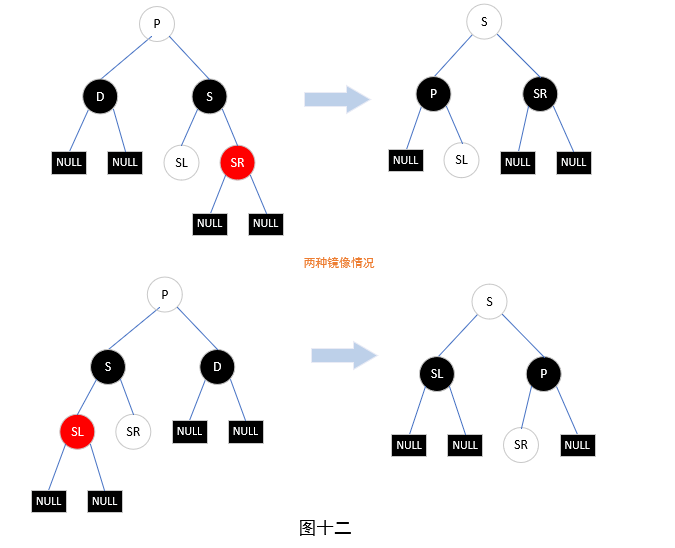
情况2 兄弟节点为黑色，近侄子节点为红色，且远侄子节点为黑色（也就只能是NULL节点）。为什么远侄子节点一定是黑色的呢，如果是红色的话，不就是第一种情况了么，所以一定是黑色，如果是黑色的话，一定是NULL节点。如图十三。调整方法是对S进行左旋，然后调换S和SL的颜色，你会发现调整后的样子就是我们上面图十二讨论的情况，只不过SL是黑色的NULL节点罢了，然后再执行一次上面那种情况的调整。

情况3 兄弟节点为黑色且兄弟节点的孩子是NULL，父节点为红色。见图十四，调整方法是删除D后，将P变成黑色，反正P的父亲肯定是黑色，不会产生冲突，然后将S染成红色，这样，路径上的黑色节点数就和原来一样了。

情况4 兄弟节点为黑色且兄弟节点的孩子是NULL，父节点为黑色，和上面那种情况很像。见图十五。我们删了一个黑色节点，剩下的也全是黑节点，这种情况下，再怎么调整也无法保持黑色路径上的黑色节点数和原来一样了。只能先暂时像情况3一样操作，然后把P当做起点，再次向上调整。

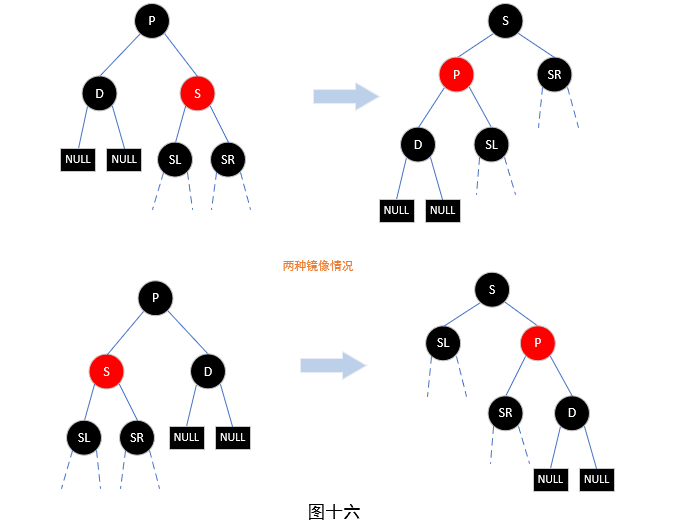
情况5 待删除节点的兄弟节点为红色。见图十六，调整方法是将兄弟节点和父节点颜色调换，然后执行一次旋转。调整后待删除节点的兄弟节点就又变成了黑色，观察下上面说的四种情况，它们的兄弟节点都是黑色，所以调整后又回到了上述四种情况之一，具体是哪一种情况，就要看调整后兄弟节点的孩子情况了。

至此，删除节点所有情况全部分析完毕。

代码实现

写完插入节点后，觉得只要细心就可以完成，所以删除操作偷懒没有写....插入是ojbk的。

红黑树的定义

const int red = 0;
const int black = 1;

class RBTree {
public:
	int color;			//颜色
	int key;			//键值
	RBTree *parent;		//父节点
	RBTree *left;		//左孩子
	RBTree *right;		//右孩子

	RBTree()
	{
		color = red;
		key = -999;
		parent = NULL;
		left = NULL;
		right = NULL;
	}
};

判断此节点是否是父节点的哪一个孩子

/*
判断此节点是否是父节点的左孩子
	1 左孩子
	0 右孩子
	-1 当前节点是根节点
*/
int isLeft(RBTree *p)
{
	if (p->parent == NULL)
	{
		return -1;
	}
	if (p == p->parent->left)
	{
		return 1;
	}
	return 0;
}

/*
红父红叔冲突，调整节点颜色
*/
void adjustColor(RBTree*& p)
{
	//祖父染成红色
	p->parent->parent->color = red;
	//祖父的两个孩子染成黑色
	if (p->parent->parent->left != NULL)
	{
		p->parent->parent->left->color = black;
	}
	if (p->parent->parent->right != NULL)
	{
		p->parent->parent->right->color = black;
	}

}

/*左旋转*/
RBTree* SingleRotateWithLeft(RBTree*& X)
{
	RBTree *P = X->parent;
	RBTree *G = P->parent;
	RBTree *U = G->right;

	RBTree* parent = G->parent;
	//查询祖父在祖父父亲的位置
	int pos = isLeft(G);
	//
	G->left = P->right;
	P->right->parent = G;
	G->parent = P;
	G->color = red;
	P->right = G;
	P->parent = parent;
	P->color = black;

	
	if (pos == 1)
	{
		parent->left = P;
	}
	else if (pos == 0)
	{
		parent->right = P;
	}
	return P;
}

/*右旋转*/
RBTree* SingleRotateWithRight(RBTree*& X)
{
	RBTree* P = X->parent;
	RBTree* G = P->parent;
	RBTree* U = G->left;
	RBTree* parent = G->parent;
	//查询祖父在祖父父亲的位置
	int pos = isLeft(G);
	G->right = P->left;
	P->left->parent = G;
	G->parent = P;
	G->color = red;
	P->color = black;
	P->left = G;
	P->parent = parent;
	
	if (pos == 1)
	{
		parent->left = P;
	}
	else if (pos == 0)
	{
		parent->right = P;
	}
	return P;
}

/*左-右双旋转*/
RBTree* DoubleRotateWithLeft(RBTree *&X)
{
	RBTree* P = X->parent;
	RBTree* G = P->parent;
	RBTree* U = G->right;
	RBTree* parent = G->parent;
	//查询祖父在祖父父亲的位置
	int pos = isLeft(G);
	P->right = X->left;
	if(X->left)
		X->left->parent = P;
	G->left = X->right;
	if(X->right)
	X->right->parent = G;
	X->left = P;
	X->right = G;
	P->parent = X;
	G->parent = X;
	X->parent = parent;
	
	if (pos==1)
	{
		parent->left = X;
	}
	else if(pos==0)
	{
		parent->right = X;
	}
	//染色
	X->color = black;
	G->color = red;

	return X;
}

/*右-左双旋转*/
RBTree* DoubleRotateWithRight(RBTree * &X)
{
	RBTree* P = X->parent;
	RBTree* G = P->parent;
	RBTree* U = G->left;
	RBTree* parent = G->parent;
	//查询祖父在祖父父亲的位置
	int pos = isLeft(G);
	G->right = X->left;
	if(X->left)
		X->left->parent = G;
	P->left = X->right;
	if(X->right)
		X->right->parent = P;
	X->left = G;
	X->right = P;
	G->parent = X;
	P->parent = X;
X->parent = parent;
	
	if (pos == 1)
	{
		parent->left = X;
	}
	else if (pos == 0)
	{
		parent->right = X;
	}
	//染色
	X->color = black;
	G->color = red;

	return X;
}

/*
调整红黑树
*/
void adjustRBTree(RBTree*& root,RBTree*& p)
{
	//父亲空指针，不需要判定
	if (p->parent == NULL)
	{
		//重新设置根节点
		root = p;
		return;
	}
	//祖父空指针，不需要判定
	if (p->parent->parent == NULL)
	{
		return;
	}
	//没有冲突，结束
	if (p->color==black||p->parent->color == black)
	{
		return;
	}
	//判断当前节点的父亲是祖父的左孩子还是右孩子
	int fPos = isLeft(p->parent);
	//红父红叔冲突
	if ((fPos==1 && (p->parent->parent->right != NULL && p->parent->parent->right->color == red))
		|| (fPos==0 && (p->parent->parent->left != NULL && p->parent->parent->left->color == red))) {
		//调整颜色即可，不需要旋转
		adjustColor(p);
		//祖宗是根节点，调整它的颜色就可以了
		if (p->parent->parent->parent == NULL)
		{
			p->parent->parent->color = black;
		}
		//将祖父节点设置为当前节点，继续调整
		else
		{
			adjustRBTree(root,p->parent->parent);
		}
	}
	//红父黑叔冲突
	else
	{
		//判断当前节点是父节点哪一个孩子
		int pos = isLeft(p);
		RBTree* result;
		//左左
		if (fPos==1&&pos==1)
	{
			result = SingleRotateWithLeft(p);
		}
		//右右
		else if (fPos==0 && pos==0)
		{
		result = SingleRotateWithRight(p);
		}
		//左右
		else if (fPos==1 && pos==0)
		{
			result = DoubleRotateWithLeft(p);
		}
		//右左
		else
		{
			result = DoubleRotateWithRight(p);
		}
adjustRBTree(root,result);
	}
}

/*
*插入节点
*/
void insert(RBTree*& root, int val)
{
	if (root == NULL)
	{
		root = new RBTree();
		root->key = val;
		root->color = black;
        	return;	}

	RBTree *t = root;
	//将要插入的节点
	RBTree *p = new RBTree();
	p->key = val;
	//先将节点插入叶子节点里
	while (true) {
		if (val > t->key)
		{
		if (t->right == NULL)
			{
				t->right = p;
				p->parent = t;
				break;
			}
			else
			{
				t = t->right;
			}
		}
		else if (val < t->key)
		{
			if (t->left == NULL)
			{
				t->left = p;
				p->parent = t;
				break;
			}
			else {
			t = t->left;
			}

		}
		else
		{
			return;
		}
	}

	//开始调整红黑树
	adjustRBTree(root,p);

}

附上cpp代码点击下载