拓扑排序

发表于 更新于 分类于

拓扑排序是对有向无圈图的顶点的一种排序，它使得如果存在一条从vi 到vj 的路径，那么排序中vj 在vi 的后面。如果图含有圈，那么拓扑排序是不可能的。此外，排序的结果不是唯一的，任何合理的排序都是可以的。

拓扑排序对应施工的流程图具有特别重要的作用，它可以决定哪些子工程要先执行，哪些子工程要在某些工程执行后才可以执行。选课课程同样如此，有些必须课必须要先修，有些要某些课程结束之后才能选修。

图的表示方法

图有两种表示方法，一种是邻接矩阵，它的空间需求是Θ(|V|²)，V为图的顶点个数。如果图是稠密的，那么这种方法是比较适合的 ，如果图是稀疏的，边的数量非常少，那么就会浪费大部分空间，这是很糟糕的，因为我们想要我们的数据结构表示那些实际存在的数据，而不是去表示不存在的数据。而大部分处理的图都是稀疏的，所以我们采用邻接表表示。邻接表是表示图的标准方法。对每一个顶点，使用一个表存放所有邻接的顶点，此时的空间需求为O(|E|+|V|)，如果是有向图，则存放的是指向的顶点。

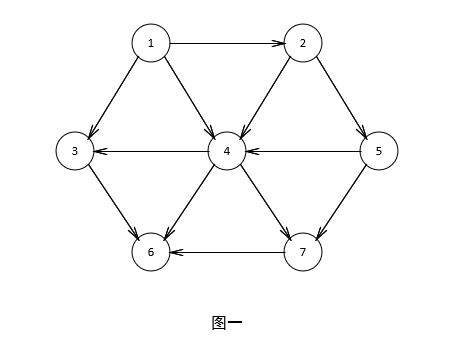
1533652891196.png

对于上面的图，使用邻接表表示法的结果为下图所示

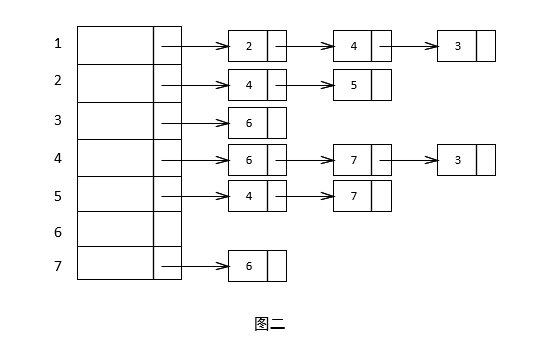
1533654312376.png

实现步骤

  1. 在有向图中选一个没有前驱，也就是入度为0 的顶点并且输出。
  2. 在图中删除该顶点以及和此顶点相关的边。
  3. 重复上述两步，直至所有顶点输出，或不存在没有前驱的节点为止。后者说明图是有环的。

观察图一，可以发现顶点1是没有前驱的，那么我们先输出1，然后删除顶点以及相关的边，得到下图。

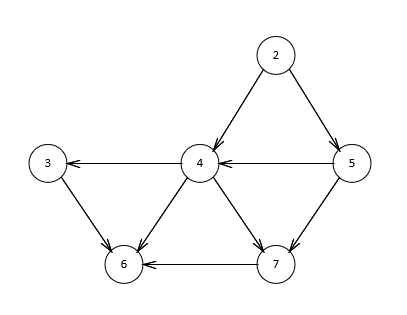
1533659652842.png

继续寻找，发现2没有前驱，那么输出2，删除顶点以及边，得到下图。

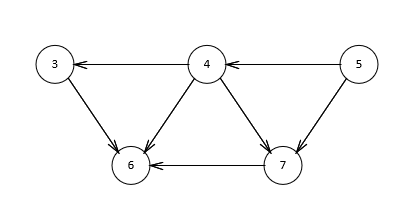
1533659700303.png

继续寻找，5没有前驱，输出此节点后，得到下图。

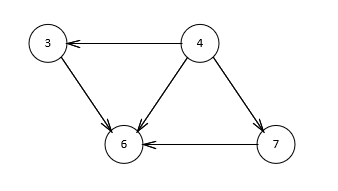
1533659733346.png

继续寻找，4没有前驱，输出它得到下图。

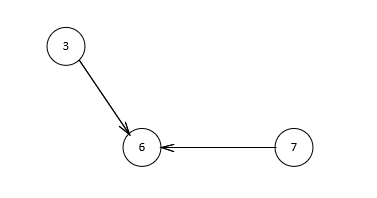
1533659761851.png

此时，3和7都是没有前驱的，随意选择一个，输出3，得到下图。

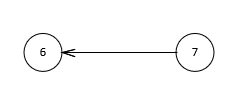
1533659808925.png

然后输出7。

1533659857398.png

最后输出6，排序结束。

对于图一，1254376和1254736都是正确的拓扑排序。

代码实现

以下内容重写于 2021年 9月25日 夜 ，原来用的 c++ ，代码、解释也比较腌臜…

上图中说得很简单，看看哪个入度为 0，就删掉对应的节点和边。那咋快速知道哪个结点的入度为 0 ？当然就用一个数组了。这次演示，我们的结点都是用 0 - N 的数字标号，所以可以简单使用 List 和 int[] 来存储。如果结点的 key 是其他规则，则应该使用 Map。

edges 表示邻接矩阵， edges.get(i) 存储的是以 i 作为头结点的其它尾结点。 indeg 表示的是每个结点的入度书。

1
2
List<List<Integer>> edges = new ArrayList<>();
int[] indeg = new int[numCourses];

我们需要先初始化 邻接矩阵 和 每个结点的入度数

1
2
3
4
5
6
7
8
9
10
11
12
// N 是一共有多少个结点，是常量入参。
for (int i = 0; i < N; ++i) {
    edges.add(new ArrayList<>());
}
for (int[] edges : prerequisites) {
    int from = edges[0];
    int to = edges[1];

    adjacencyMatrix.get(from).add(to);
    // 入度 +1
    indeg[to]++;
}

接下来，要初始化队列，将所有入度为 0 的结点都先加入队列

1
2
3
4
5
6
Queue<Integer> zeroInDegreeQueue = new ArrayDeque<>();
for (int i = 0; i < N; i++) {
    if (indeg[i] == 0) {
        zeroInDegreeQueue.add(i);
    }
}

然后呢，就是不停地遍历队列直至为空，每次取出一个头结点，将相关尾结点的入度数 -1，如果 0 了，再将尾结点加入到队列中。你应该很清楚了，这就是个 BFS。

1
2
3
4
5
6
7
8
9
while (!zeroInDegreeQueue.isEmpty()) {
    Integer nowVisit = zeroInDegreeQueue.poll();
    List<Integer> tos = adjacencyMatrix.get(nowVisit);
    for (Integer to : tos) {
        if (--indeg[to] == 0) {
            zeroInDegreeQueue.add(to);
        }
    }
}

到这里基本就差不多了。但是不是忘记了什么？
怎么判断是否可以进行拓扑排序（即无环），假如可以，则排序结果呢，在哪？

排序结果我们只需要再用一个 ans 数组，每次从队列取出队头元素进行访问的时候，将其加入到 ans 中，即可。

如何判断是否有环？你可以在最后再遍历一下 indeg 数组，只要有一个入度不为 0 的，则有环；或者每次访问队列的元素的时候用个计数器数数，如果最后和 N 不一致，则说明有元素的入度不为 0。