最短路径问题（无负边值）——Dijkstra算法

发表于 更新于 分类于

Dijkstra算法使用了广度优先搜索解决了赋权有向图或无向图的单源最短路径问题。算法采用了贪心策略，分阶段的求解这个问题，这篇文章，我们进行详细的介绍。

这篇文章中，我们以图1.1中的赋权图作为示例。箭头上的数字为权值，圆圈中的字母为顶点中的数据，这里用一个字母表示。

1534060079132.png

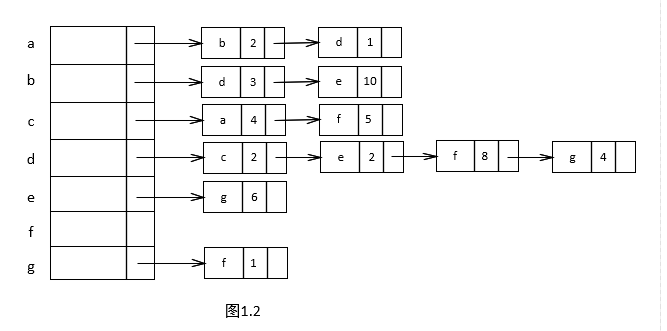
我们依旧使用邻接表来表示图，那么上图中的有向图可以表示为图1.2的样子，如果不理解，可以看上篇拓扑排序中的内容。

1534060198241.png

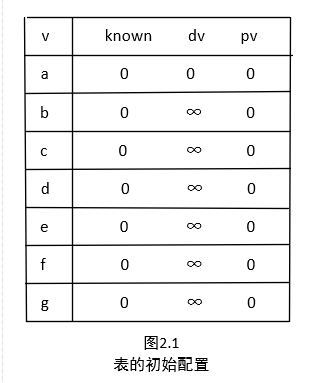
实现步骤

首先，我们需要对每个顶点进行标记，每个顶点标记为Known（已知）的，或者标记为unKnown（未知的）。同时，每个顶点需要保留一个临时距离 dv 。这个距离实际上是使用已知顶点作为中间顶点从开始顶点 s 到 v 的最短路径的长。最后，我们记录 pv ，它是引起 dv 变化的最后的一个顶点。假如开始顶点 s 是 a ，那么用于Dijkstra算法的表的初始配置应当如图2.1所示。

1534064213351.png

Dijkstra算法按阶段进行，在每个阶段，Dijkstra算法选择一个顶点 v ，它在所有未知顶点中具有最小的dv，同时算法声明从 s 到 v 的最短路径是已知的。阶段的其余部分由dw值的更新工作组成。

图2.1表示我们初始配置，且开始节点为 s 为 a。

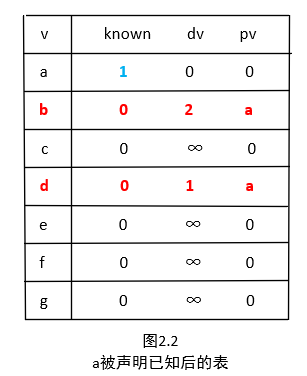
第一个选择的顶点是 a ，因为它在所有未知的顶点中具有最小的 dv ，dv 为0。将 a 标记为已知。既然 a 已知，那么某些表项就需要调整。观察图1.1，发现邻接到 a 的顶点有 b 和 d 。那么这两个顶点的项需要调整，调整后如图2.2所示。

1534065162883.png

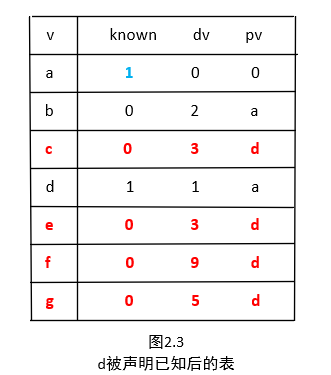
继续选择一个未知的且具有最小 dv 的顶点，也就是 d ，顶点  c，e，f，g 是邻接的顶点，而且它们实际上都需要调整，如图2.3所示。

1534065701993.png

下一个被选取的顶点是 b ，其值为 2。d 是邻接的点，但已经是已知的，因此不必做对其做工作了。 e 也是邻接的点但不需要调整，因为结果 b 的值为 2+10=12。大于 e 已知的长度为3的路径。图 2.4指出这些顶点被选取以后的表。

1534066134468.png

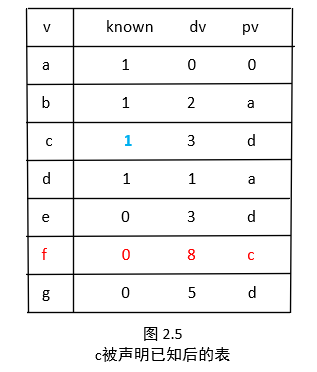
下一个被选取的点为 c，其值为3 ，a 是邻接的点，但已知，不需要处理了。f 是邻接的点，因为 3+5<9,所以需要进行调整，如图 2.5所示。

1534066489981.png

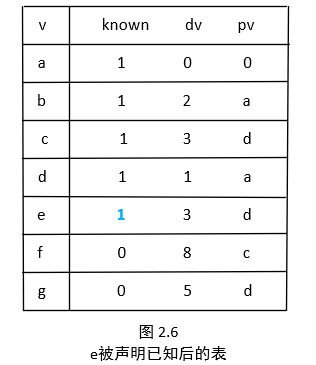
下一个被选取的点是 e ，g 是唯一的邻接顶点，但不需要调整，因为 3+6>5。结果如图 2.6所示。

1534066684105.png

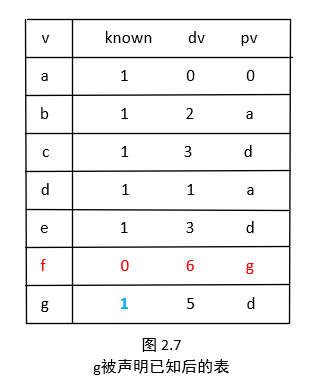
接着我们选取 g 。邻接的顶点只有 f ，因为 5+1<8，所以对 f 的距离需要下调到 6 。结果如图 2.7所示。

1534066812531.png

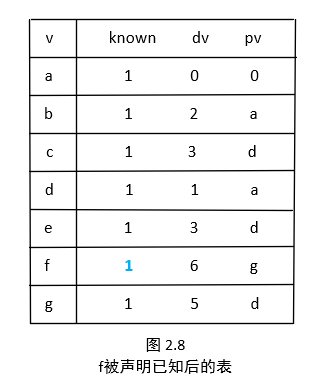
最后，我们选择顶点 f ，但其余所有顶点都已知，算法终止。最后的表在图 2.8中表出。

1534066911842.png

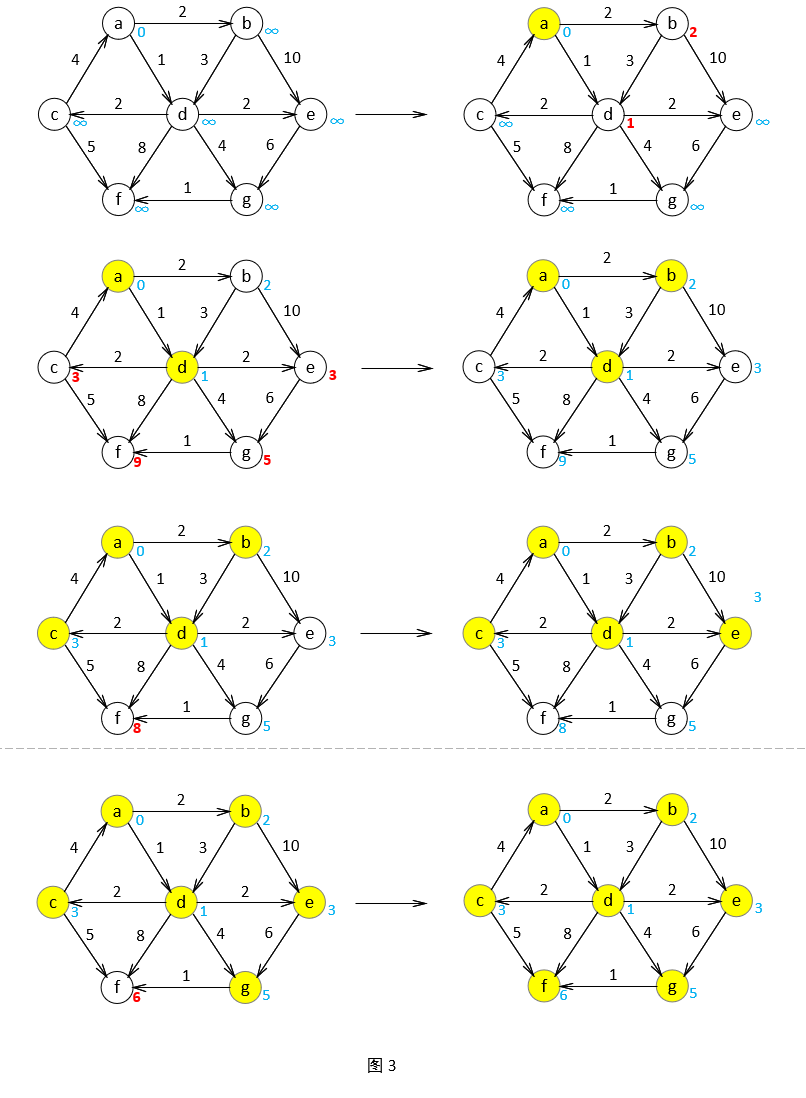
图3通过图形演示了在Dijkstra算法期间各边是如何标记为已知的以及顶点是如何更新的。顶点染成黄色说明此顶点标记为已知。

1534077874692.png

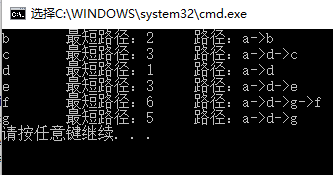
在算法结束后，我们最终得到了一张表（图 2.8）。在这张表里面，我们可以得到我们想得到的一切。例如 a 到 f 的最短路径为6。那么如何得到 a 到 f 的实际路径呢？我们可以编写一个递归来跟踪 pv 留下的痕迹。引起 f 的 dv 变化的最后的一个顶点是 g ，那么查询 g ；引起 g 的 dv 变化的最后的一个顶点是 d ，继续查 d ；引起 d 的 dv 变化的最后的一个顶点是 a ，也就是我们的开始节点，不需要继续查了， a 到 f 的最短路径就是 a->d->g->f 。 

代码实现

首先是图的顶点结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
typedef string vertex;
struct Node
{
	vertex data;
	int weight = 0;
	Node *next = NULL;

	Node(vertex data,int weight, Node *next = NULL)
	{
		this-&gt;data = data;
		this-&gt;weight = weight;
		this-&gt;next = next;
	}
};

其次，我们还需要维护一个像上面的表，有known，dv，和pv。
表 不考虑负边

1
2
3
4
5
6
7
const int INFINITE = -1;  //距离 定义无限大
struct Box
{
	bool known = false;
	int dv = INFINITE;
	vertex path;
};

和上一篇拓扑排序中使用的方法一致，还是使用map来存储，比较方便。

直接给出代码，关键地方都已经打好注释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
map<vertex, Box> Dijkstra(vertex v,map<vertex, Node> graph)
    {
    	map<vertex, Box> boxs = initBox(v, graph);
    	while (1)
    	{
    		map<vertex, Box>::iterator it = boxs.begin();
    		int min = 99999999;
    		//key为当前阶段应当标记为已知的顶点
    		vertex key;
    		int flag = 0;
    		while (it != boxs.end())
    		{
    			if (it->second->known==false&amp;&amp; it-&gt;second-&gt;dv!= INFINITE &amp;&amp;it-&gt;second-&gt;dv &lt; min)
    			{
    				min = it-&gt;second-&gt;dv;	//记录最短路径
    				key = it-&gt;first;		//记录最小路径的key
    				flag = 1;				//将flag置为1，说明，还有known为false的
    			}
    			it++;
    		}
    		//所有known都是true ，算法结束
    		if (flag == 0)
    		{
    			return boxs;
    		}

    		boxs[key]-&gt;known = true;		//将最小的顶点known置为true

    		//将所有与此顶点相邻接的点进行更新
    		Node* n = graph[key];
    		while (n != NULL)
    		{
    			//如果此顶点是已知的，就不虚要再处理了
    			if (boxs[n-&gt;data]-&gt;known == true)
    			{
    				n = n-&gt;next;
    				continue;
    			}
    			//此顶点计算出来到it2的路径
    			int d_new = boxs[key]-&gt;dv + n-&gt;weight;
    			//原本it2的路径长度
    		int d_old = boxs[n-&gt;data]-&gt;dv;

    			//需要更新
    			if (d_old == INFINITE || d_new &lt; d_old)
    			{
    		boxs[n-&gt;data]-&gt;dv = d_new;
    				boxs[n-&gt;data]-&gt;path = key;
    			}
    			n = n-&gt;next;
    		}
    	}
    }`</pre>

    输出算法的结果
    <pre>`string printp(vertex p, map&lt;vertex, Box*&gt; boxs)
    {
    	if (boxs[p]-&gt;dv == 0)
    	{
    		return p+"";
    	}
    	return printp(boxs[p]-&gt;path, boxs) + "-&gt;" + p;
    }
    //输出算法的结果
    map&lt;vertex, string&gt; printfDijkstra(map&lt;vertex, Box*&gt; boxs)
    {
    	//用来存放输出的内容
    	map&lt;vertex, string&gt; outs;
    	vertex aim;
    	//找到起点
    	map&lt;vertex, Box*&gt;::iterator it = boxs.begin();
    	while (it != boxs.end())
    	{
    		if (boxs[it-&gt;first]-&gt;dv == 0) {
    			aim = it-&gt;first;
    			break;
    }
    		it++;
    	}
    	it = boxs.begin();
    	while (it != boxs.end())
    	{
    		if (it-&gt;first != aim)
    		{
    			string path = printp(boxs[it-&gt;first]-&gt;path, boxs) + "-&gt;" + it-&gt;first;
    			outs.insert(pair&lt;vertex, string&gt;(it-&gt;first, path));
    	}

    		it++;
    	}
    	//outs已经存放好所有路径了
    	//打印数据
    	it = boxs.begin();
    	while (it != boxs.end())
    	{
    		if (it-&gt;first != aim)
    		{
    			cout &lt;&lt; it-&gt;first + "\t最短路径：" + to_string(boxs[it-&gt;first]-&gt;dv) + "\t路径：" + outs[it-&gt;first] &lt;&lt; endl;
    		}
    		it++;
    	}
    	return outs;
    }

1534089759880.png

完整测试代码