通俗易懂地讲解概率论
几个基础公式
条件概率
指事件 A 在事件 B 已经发生的条件下发生的概率,公式为:
$$P(A|B) = \frac{P(AB)}{P(B)}$$
全概率
作用在于将复杂事件的概率求解转化为在不同情况下发生的简单事件的概率求和
$$
P(A) = \sum_{i=1}^N P(A | B_i) * P(B_i) \\
\sum_{i=1}^N P(B_i) = 1
$$
联合概率
上式中 P(AB) 称为联合概率,表示 A 和 B 两个事件共同发生的概率,如果两个事件是相互独立的,那么有 $ P(AB) = P(A) · P(B) $,还有 $ P(A|B) = P(A) $
P(A,B) 或者 P(A∩B) 也都是联合概率的表达方式。
贝叶斯定律
公式:
$$P(H | D) = \frac{P(D | H) · P(H)}{P(D)}$$
来理解一下出现的几个定义:
- P(H),H 的先验概率,即预先设定的假设成立的概率。
- P(D | H),H 的似然概率 $l(H | D)$,是在假设成立的前提下观测到结果的概率。
- P(H | D),H 的后验概率,即在观测到结果的前提下假设成立的概率。
举个 🌰
由于定义从不说人话,大部分人第一次看见这个都一脸懵逼,下面结合一个 🌰 来理解:
国人玩游戏的概率为 P(✔️) = 0.6,不玩游戏的概率为 P(✗) = 0.4,这个概率是统计得到的,或者是自身根据经验给出的一个概率值,我们称这个为先验概率。
另外,玩游戏的人中男性的概率为 P(M | ✔️) = 0.8,女性的概率为 P(F | ✔️) = 0.2。
我们可以写出对应的条件概率分布:
P(M | ✔️) = 0.8, P(M | ✗) = 0.2
P(F | ✔️) = 0.2, P(F | ✗) = 0.8
严格来讲,P(M | ✔️) = 0.8 并不能推导出 P(M | ✗) = 0.2,但我们先做出这个假设。
现在想知道一个男性玩游戏的概率是多少? 即 P(✔️ | M) 的值,这就是后验概率。
根据贝叶斯公式和全概率公式可得
\begin{split}
P(✔️ | M) &= \frac{P(M | ✔️) · P(✔️)}{P(M)} \\
&\quad= \frac{P(M | ✔️) · P(✔️)}{P(M | ✔️) · P(✔️) + P(M | ✗) · P(✗)} \\
&\quad= \frac{0.8 * 0.6}{0.8 * 0.6 + 0.2 * 0.4} \\
&\quad= 0.857 \\
\end{split}
再理解
结合 🌰 理解一下,可以有个大概印象:
先验概率
先验概率是以全事件为背景下,✔️ 事件发生的概率,即 P(✔️ | Ω)
全事件一般是统计获得的,所以称为先验概率,没有实验前的概率。
Ω:样本空间,概率论和统计力学中所有可能的事件或系统状态的集合
后验概率
后验概率是以新事件 M 为背景下,✔️ 事件发生的概率,即 P(✔️ | M),计算的是在给定 M 后,✔️ 发生的概率。实际上就是条件概率。
新事件一般是试验,如试验B,此时的事件背景从全事件变成了B,该事件B可能对A的概率有影响,那么需要对A现在的概率进行一个修正,从P(A|Ω)变成 P(A|B),所以称 P(A|B)为后验概率,也就是试验(事件B发生)后的概率。
似然概率
在这个例子中,P(✔️ | M) 是后验概率, P( M | ✔️) 是似然概率。
P(✔️ | M) 是给定参数男性,他玩游戏的可能性,关注的是事件 ✔️ 的发生概率。
如何理解似然呢?P( M | ✔️),是玩游戏的人是男性的概率。
P(✔️ | M) 是一个有两个变量的函数, 将 M 看作为常量,则会得到一个概率函数;将 ✔️ 看作常量,会得到一个似然函数(关于 M 的函数)。
P(✔️ | M) 是 M 参数下 ✔️ 出现的概率,同时也是 ✔️ 出现时 M 参数的靠谱程度,也就是 M 的似然。
**极大似然估计 (ML估计)**,就是在已知观测的数据的前提下,找到使得似然概率最大的参数值。
再谈似然函数
公式
设已知样本集为 $D={x_1, x_2, ··· , x_n}$,
参数 θ 的似然函数为 $l(θ) = P(D | θ) = P(x_1, x_2, ··· , x_n | θ) = \prod_{i=i}^nP(x_i | θ)$
如果说 $θ_0$ 是能使似然函数 $l(θ)$ 取得最大值的 $θ$ 值,则应该 $θ_0$ 是最可能的参数值,那么 $θ_0$ 就是 $θ$ 的极大似然估计量。
max 和 argmax 的区别 ?设 y = f(x) 是一般的函数式
y = max f(x)代表:y 是 f(x) 函数所有值中最大的。
y = argmax f(x)代表:y 是 f(x) 函数中,会产生最大值的那个参数 x。arg 即 argument,此处意为“自变量”。
举个 🌰
拿抛硬币这个例子来说,一枚均匀硬币的正面概率是 $p = 0.5$,正面朝上记作 $H$ ,反面朝上记作 $T$,现在要预测抛三次,结果是 $HHT$ 的概率。
$$
data = (x_1, x_2, x_3) = (H, H, T)\\
P(HHT ; p=0.5) = \prod_{i=i}^3P(x_i ; p=0.5) = 0.5 * 0.5 * 0.5 = 0.125
$$
如果说正面朝上的概率 $p = 0.4$ ,那么 $P(HHT ; p=0.4) = 0.4 * 0.4 * 0.6 = 0.096$
似然概率正好与这个过程相反,我们关注的量不再是事件的发生概率,而是已知发生了某些事件,我们希望知道参数应该是多少。
现在我们已经抛了三次硬币,并且知道了结果是两次正面,一次反面,这时候,我们希望知道这枚硬币抛出去正面朝上概率为 0.5 的概率是多少?正面朝上概率为 0.8 的概率是多少?
如果我们希望知道正面朝上概率为 0.5 的概率,这个东西就叫似然概率,可以说是对某一个参数猜想 $p = 0.5$ 的概率。这样表示成条件概率就是:
$$
l(p=0.5 | HHT) = P(HHT ; p=0.5) = 0.125\\
l(p=0.4 | HHT) = P(HHT ; p=0.5) = 0.096
$$
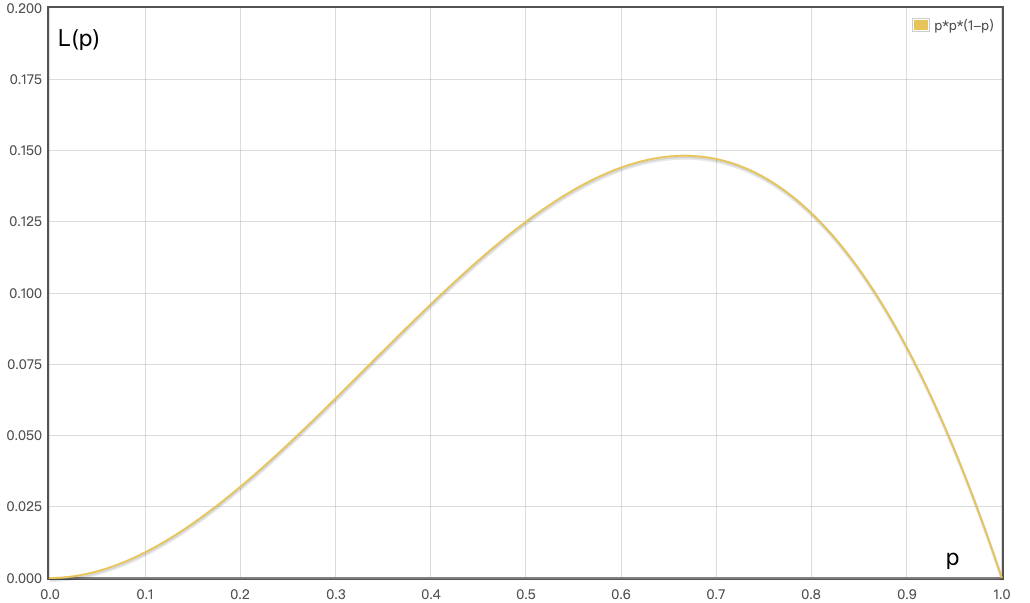
我们可以写出似然函数 $l(p | HHT) = P(HHT ; p) = p · p · (1-p) = -p^3+p^2$ ,做出函数图像如下,大约在 $p = 0.67$ 左右能够取得最大值,因此如果出现 $HHT$ ,正面朝上的概率 p 最可能是 0.67,这是最合理的数,但未必符合真实情况,因为数据量不足的缘故。
参考文章:
https://zh.wikipedia.org/wiki/后验概率
https://www.zhihu.com/question/54082000/answer/1640044106
似然和似然函数详解 https://zhuanlan.zhihu.com/p/42598338