阿烫的后花园

最近两天又闲得慌了，学习了一下爬虫。爬虫，久闻大名，如雷贯耳，总觉得是个很牛逼的东西，难度不小。学了两天下来，发现是很牛逼，但是难度真的不大。

在学习之前，一片空白。大约一年前看过廖雪峰的Python教程，现在估计也忘得差不多，如果你也是Python小白的话，去看下廖雪峰的Python教程吧。花了小半天时间复习了一下Python，这门语言入门还是很简单的，如果有其它语言的基础，大约一个小时就能写点东西出来了。

那么我们再去查Python环境下如何实现爬虫，发现一个特别特别强大的框架——scrapy，那我们就用它了。嗯？网上不是说有很多东西么？urllib、urllib2、bs4、pyspider、beautifulsoup什么什么的？一张图你就懂了

先了解下爬虫的原理。

如果我们把互联网比作一张大的蜘蛛网，数据便是存放于蜘蛛网的各个节点，而爬虫就是一只小蜘蛛，沿着网络抓取自己的猎物（数据）爬虫指的是：向网站发起请求，获取资源后分析并提取有用数据的程序从技术层面来说就是 通过程序模拟浏览器请求站点的行为，把站点返回的HTML代码/JSON数据/二进制数据（图片、视频） 爬到本地，进而提取自己需要的数据，存放起来使用。
爬虫是通过网页的链接地址来寻找网页的。从网站某一个页面（通常是首页）开始，读取网页的内容，找到在网页中的其它链接地址，然后通过这些链接地址寻找下一个网页，这样一直循环下去，直到把这个网站所有的网页都抓取完为止。如果把整个互联网当成一个网站，那么爬虫就可以用这个原理把互联网上所有的网页都抓取下来。

废话不多说，我们直接开工，首先装环境，我装的Python3.6版本，win10系统。Python安装完成之后，前往pip的官网https://pip.pypa.io/en/stable/installing/，安装pip，提供了一个get-pip.py文件，下载之后运行即可。

_pip_是一个现代的，通用的 Python 包管理工具。提供了对 Python 包的查找、下载、安装、卸载的功能。

打开cmd，输入 pip -V ，检查pip版本，没有问题后开始安装scrapy，指令为 pip install scrapy ,安装完成之后，cmd输入 scrapy version,可以查看版本号，我使用的是1.5。

之后我们还要用到mysql，这里也顺便把包安装好，指令为 pip install pymysql。

现在我们需要创建一个scrapy的工程，在自己想建立工程的位置运行cmd，输入 scrapy startproject HelloScrapy, HelloScrapy是我们的工程名。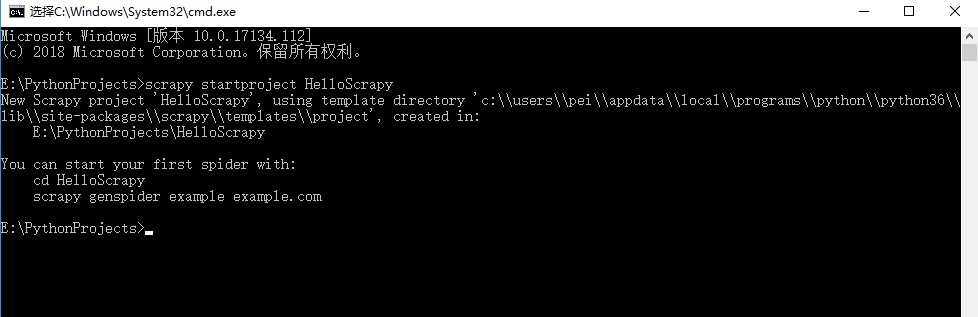

接下来，我们用PyCharm，打开我们创建的这个工程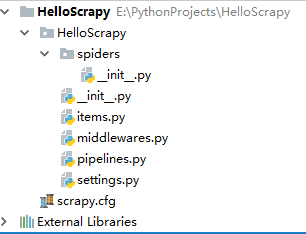

查看目录结构，scrapy为我们生成了很多东西，spiders文件夹下放的是我们写的爬虫代码，items.py是用来定义我们所需要获取的字段piplines.py是用来定义我们的存储，settings.py是定义的各种设置。现在不懂没关系，反正我们之后会用到，写一写就明白了。

现在，我们要做一件事，在根目录里，新建一个entrypoint.py文件，里面输入以下代码

1
2

from scrapy.cmdline import execute
execute(['scrapy', 'crawl', 'dingdian'])

因为Scrapy默认是不能在IDE中调试的，以后我们直接运行这个py文件就可以跑整个项目。

现在我们的项目应该是这样的

第二行中代码中的前两个参数是不变的，第三个参数是自己的spider的名字。

可是，我哪里来的myspider…别急，我们现在就来建立。首先，我们先找个爬取的目标——顶点小说，(对不住了) 现在的域名是www.x23us.com（此网站域名经常变化，谷歌搜顶点小说就好） ，那么我们在IDE里面打开terminal 输入 scrapy genspider myspider www.x23us.com 回车之后，scrapy就会用模板给我们自动生成一个爬虫

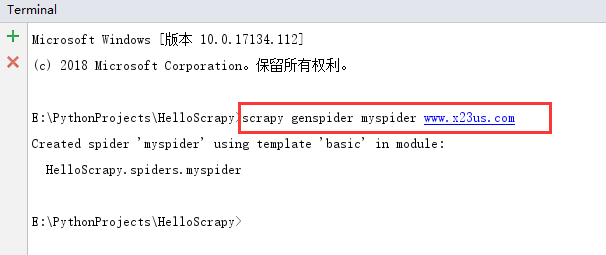
查看项目结构，多了一个文件，还有一些代码。

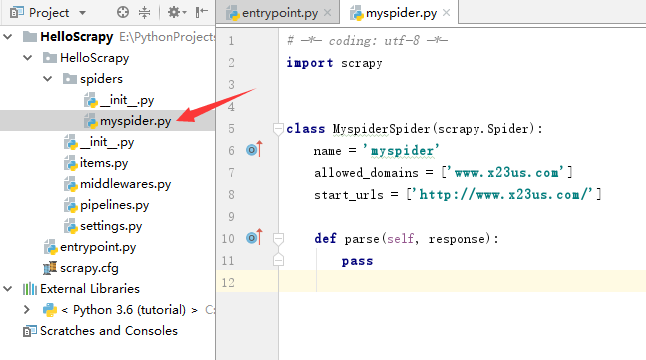
其中，name这个字段就是我们的spider的名字，整个项目不可重复。
allowed_domains这个字段是用来过滤爬取的域名，如果一不小心爬到别的地方了，就可以通过这个字段过滤掉。
start_urls就是我们第一个爬取的起始地址，这是一个list，所以可以起始地址可以有很多个。

还有一个parse方法，每个网页请求成功之后，都会调用这个方法进行处理。

爬取一个网站，肯定要先分析它是如何组成的 。

打开首页，有很多分类，自己一个个点开会发现url后缀的变化，2_1.html,3_1.html,4_1.html等等。那么爬虫的入口地址就有了

玄幻魔幻：http://www.x23us.com/class/1_1.html

武侠修真：http://www.x23us.com/class/2_1.html
都市言情：http://www.xx23us.com/class/3_1.html
历史军事：http://www.x23us.com/class/4_1.html
侦探推理：http://www.x23us.com/class/5_1.html
网游动漫：http://www.x23us.com/class/6_1.html
科幻小说：http://www.x23us.com/class/7_1.html
恐怖灵异：http://www.23wx.com/class/8_1.html
散文诗词：http://www.23wx.com/class/9_1.html
其他：http://www.23wx.com/class/10_1.html

入口有两种写法，一种是用start_urls变量，直接把上述的url地址放进去，但是不太美观。还有一种是重写start_requests函数，重写这个函数之后，start_urls就不起作用了，我使用的后者，将地址拼接出来了。

现在运行entrypoint.py

可以看见控制台输出了一大堆日志

看见这些，就说明OK了。

现在我们要遍历所有的页面来获取所有小说

每个分类下面可以看到总页数，我们获取每个分类的总页数，然后循环，理论上就可以拿到所有页面了。如何获得这个总页数？这就需要用到xpath，找到这个元素在html的位置。不知道什么是xpath？没关系，多用用就明白了，没什么复杂的（其实我也不懂啥事xpath - -！）。我使用的谷歌浏览器，右键单击上图中的106

点击最下面的检查

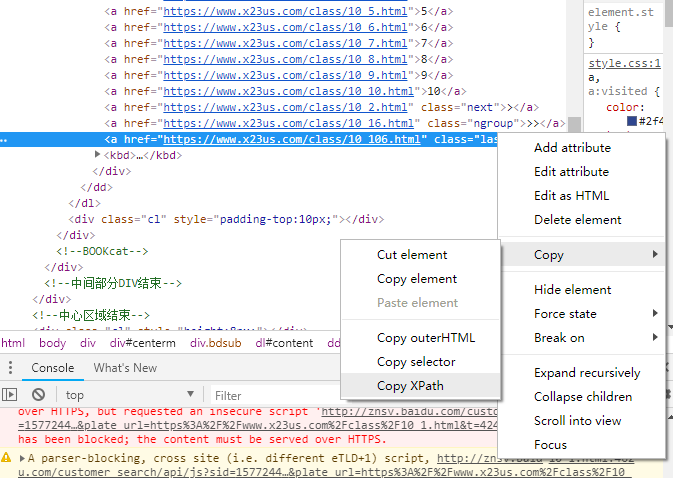
右键单击蓝色高亮的代码，Copy -> Copy XPath 就能拿到位置，复制到的是

1

//*[@id="pagelink"]/a[14]

想要拿到它里面的值需要这样

1

response.xpath("//*[@id='pagelink']/a[14]/text()").extract_first()

/text()能够获得里面的值，response.xpath() 返回的是一个list，使用，如果列表里只有一个元素，使用extract_first()来提取，如果list里面有多个元素，就必须要使用extract()来获取全部元素。

我们构造完URL之后继续调用Reques，回调函数为parse_name()

我们要拿到每一个小说的名称和作者，和拿到最大值的流程一样，懒癌犯了，直接贴代码…..

分别获得三个列表，然后for循环一个个取出来，发现多了一个meta字典，这是Scrapy中传递额外数据的方法，因我们还有一些其他内容需要在下一个页面中才能获取到。

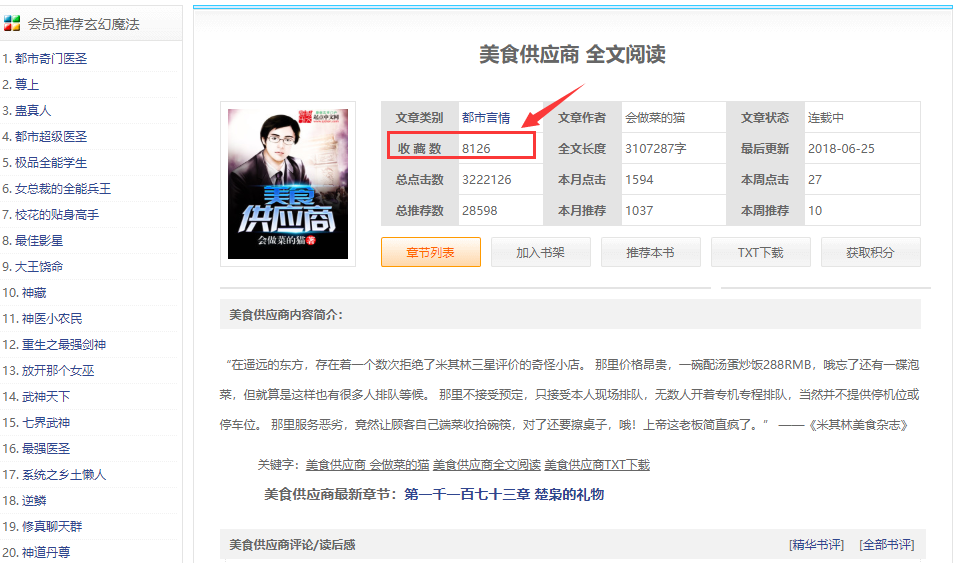
现在我们的爬虫到了这个页面，这个页面我们就取一个收藏数吧

1

collect_num_str=response.xpath('//*[@id="at"]/tr[2]/td[1]/text()').extract_first()  # 网页中含有<span style="color: inherit; font-size: inherit;"> 空格 ==> \xa0</span>``collect_num=int("".join(collect_num_str.split())) #去掉空格的编码 收藏数

pre宋体';font-size:10.5pt;"这里有个要注意的地方，网页中含有 ，我们提取出来的/pre宋体';font-size:10.5pt;"collect_num_str含有\xa0，我们需要去掉它。

至今为止我们，已经抓取了我们想要的内容了，小说名称，作者，链接，收藏数。上面的代码都打印出来了。

现在我们需要存到数据库里面。这时候我们需要编辑item.py了

写下这四个我们所需的字段。

在根目录下新建mysqlpiplines文件夹，文件夹下面建立sql.py。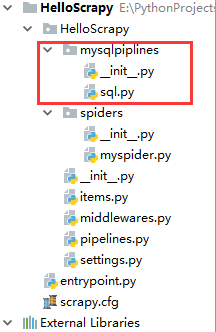

我们要在sql.py里面编写我们的sql语句。打码的四个变量写上你自己的。

主要写了两个方法，一个插入，一个根据小说名称判断是否已经存在。

现在编辑piplines.py

接着我们修改一下我们的爬虫代码。

把我们拿到的数据传给item，剩下的就不需要我们做了。

最后一步，打开settings.py,关掉ITEM_PIPELINES的注释

这个300是优先级，现在不需要管它，关闭掉注释就可以了。

我们跑下项目，爬虫已经可以开始正常工作

大约爬了三十分钟，抓起了三万八千多条记录。是不是特别强大？

https://github.com/peihuanhuan/dingdian

在做java web云盘的时候，遇到了一个诡异的错误。用户注册时，需要用ajax判断该邮箱是否被注册。一开始没有发现问题，有一次测试注册的时候，却发现邮箱验证出现了异常，浏览器F12打断点，ajax请求直接进了error，后台打断点也没有进入。返回的error是一大串html代码，完全让我摸不着头脑。

开始检查dataype，data，url，没有错误啊。还是不行，开始去网上搜偏方子，试了很多方法，都是错误，只不过报错不一样了。。。于是很纳闷，老子写过那么多ajax了，什么样的请求没遇见过？验证邮箱这种请求，就给一个参，返回一个true or false ，哪里有理由出错？之后继续调试，发现必须要随便登录过一个账号，然后再返回注册，这个ajax才能正常请求。瞪了快半个晚上还是没有没看出来原因，就先放一边了。

今天在测试Android的请求时候，再次写了一下这个请求，本来想扔在浏览器敲回车，看看返回的是不是我想要的数据格式，结果跳转到了登录页面？恍然大悟，后台做了拦截器，拦截了所有controller，除了登录的controller请求，如果没有session（没登录），就跳转到登录页面。所以必须要登录之后才能注册的原因是这个，我把邮箱验证也给拦截掉了。修改下代码，问题解决。

红黑树（red black tree）是AVL树的一个变种，如果还不是十分了解AVL树，建议先读一下之前写的平衡二叉树的文章。 平衡二叉树（AVL树）的实现

红黑树是具有下列着色性质的二叉查找树：
1.每一个节点或者着成红色，或者着成黑色；
2.根是黑色的；
3.如果一个节点是红色的，那么它的子节点必须是黑色的；
4.从一个节点到一个NULL指针的每一条路径必须包含相同数目的黑色节点。

自底向上插入的过程

图二是对图一插入25的结果，父节点为黑色，无冲突，不需要调整。

在继续讲解之前，必须要确认一下各节点的叫法

以下是两种冲突情况

1.红父红叔

有一种特殊情况，如图四调整后的就是我们的红黑树，也就是说G是根节点，那么此时的调整方法是将G染成黑色即可。

我们对图二插入54的结果如下，当前节点由54变为了50。

2.红父黑叔

剩下两种镜像情况

现在对图五的红黑树进行再次调整，调整结果见图八，图中已经标注了X、P、G、U，不理解的再看看上面两张图。其余情况不再举例了。

红黑树的插入操作不是很复杂，这里强烈建议你自己写一些数字然后按照上面的插入过程一个个走一遍，这样印象会非常深刻，也能更加深入的了解这个过程，你一定会感叹，红黑树真是巧妙。例如：10，5，6，16，1，11，12，21，15，17，14 按顺序插入的最终结果如图九所示。

自底向上删除的过程

总体上来看分为两大步

第一步，将红黑树当一棵普通的二叉查找树，将节点删除

case 1：被删除的节点是叶子节点，直接删除节点。
case 2：被删除的节点只有一个孩子，不管是左孩子还是右孩子，删掉节点后，用孩子代替删除的节点
case 3：被删除的节点有两个孩子，先查找到这个节点的后继节点，（比它大的最小节点），用后继节点的值替代想要删除节点的值（想要删除的节点颜色不需要改变），然后删除掉后继节点。这样又巧妙地将问题转化为删除后继节点的情况了。因为删除后继节点，一共只有两种情况，要么为叶子节点，要么为只有一个有孩子的节点，不可能出现其它情况。这两种情况也就是case 1和case 2。

第二步，通过旋转和染色等一系列操作，使之重新成为一棵红黑树

下面开始详细分析。由第一步，不难明白，其实只要讨论删除的节点是叶子节点或只有一个孩子就可以。

case 2 比较简单，只有一种情况，当然要是细分的话，也可以分为两种镜像情况。这种情况是想要删除的节点为黑色，而且唯一的孩子是红色，当然，孩子的位置是无所谓的。为什么唯一的孩子是红色呢，因为如果是黑色，肯定会违反性质4。那为什么想要删除的节点不能为红色呢？那么我们假设想要删除的节点为红色，当然它也只有一个孩子，假如这个孩子是红色的，不管是左孩子还是右孩子，肯定都违反了红节点不能有红色儿子的要求（性质3）。假如这个孩子是黑色的，不管是左孩子还是右孩子，肯定违反了性质4。所以想要删除的节点不可能是红色。调整方法，简单明了，孩子替换父亲，并且染成黑色即可。见图十,D是我们想要删除的节点，P代表它的父节点，没有颜色说明什么颜色都可以，和D垂直，说明D是P的左孩子还是右孩子没有关系。

case 1 分为两大类，第一类，叶子节点是红色，直接删除，结束（见图十一）。额？这也算一个大类，其实是因为下一类情况特别麻烦

第二类，想要删除的叶子节点是黑色。这个可就要分为好多种情况了。

情况1 兄弟节点为黑色，且远侄子节点为红色。见图十二，没有上色说明什么颜色都可以。SL无论黑色红色都属于这种情况。（注意：如果SL是黑色的话，那么它一定是空节点NULL；如果SL是红色的话，那么它肯定和SR一模一样，只有有两个黑色的NULL节点）

对于这种情况，删除掉D后，有一边会少了一个黑色节点，但有一个侄子是红色的，那么我们可以通过旋转和染色重新完成平衡，这个过程在P的内部就可以解决，所以和P的颜色无关。调整过程为将P和S的颜色互换，然后进行一次右旋，最后将SR染成黑色即可。（以第一种情况说明）

情况2 兄弟节点为黑色，近侄子节点为红色，且远侄子节点为黑色（也就只能是NULL节点）。为什么远侄子节点一定是黑色的呢，如果是红色的话，不就是第一种情况了么，所以一定是黑色，如果是黑色的话，一定是NULL节点。如图十三。调整方法是对S进行左旋，然后调换S和SL的颜色，你会发现调整后的样子就是我们上面图十二讨论的情况，只不过SL是黑色的NULL节点罢了，然后再执行一次上面那种情况的调整。

情况3 兄弟节点为黑色且兄弟节点的孩子是NULL，父节点为红色。见图十四，调整方法是删除D后，将P变成黑色，反正P的父亲肯定是黑色，不会产生冲突，然后将S染成红色，这样，路径上的黑色节点数就和原来一样了。

情况4 兄弟节点为黑色且兄弟节点的孩子是NULL， 父节点为黑色，和上面那种情况很像。见图十五。我们删了一个黑色节点，剩下的也全是黑节点，这种情况下，再怎么调整也无法保持黑色路径上的黑色节点数和原来一样了。只能先暂时像情况3一样操作，然后把P当做起点，再次向上调整。

情况5 待删除节点的兄弟节点为红色。见图十六，调整方法是将兄弟节点和父节点颜色调换，然后执行一次旋转。调整后待删除节点的兄弟节点就又变成了黑色，观察下上面说的四种情况，它们的兄弟节点都是黑色，所以调整后又回到了上述四种情况之一，具体是哪一种情况，就要看调整后兄弟节点的孩子情况了。

至此，删除节点所有情况全部分析完毕。

代码实现

写完插入节点后，觉得只要细心就可以完成，所以删除操作偷懒没有写....插入是ojbk的。

红黑树的定义

const int red = 0;
const int black = 1;

class RBTree {
public:
	int color;			//颜色
	int key;			//键值
	RBTree *parent;		//父节点
	RBTree *left;		//左孩子
	RBTree *right;		//右孩子

	RBTree()
	{
		color = red;
		key = -999;
		parent = NULL;
		left = NULL;
		right = NULL;
	}
};

判断此节点是否是父节点的哪一个孩子

/*
判断此节点是否是父节点的左孩子
	1 左孩子
	0 右孩子
	-1 当前节点是根节点
*/
int isLeft(RBTree *p)
{
	if (p->parent == NULL)
	{
		return -1;
	}
	if (p == p->parent->left)
	{
		return 1;
	}
	return 0;
}

/*
红父红叔冲突，调整节点颜色
*/
void adjustColor(RBTree*& p)
{
	//祖父染成红色
	p->parent->parent->color = red;
	//祖父的两个孩子染成黑色
	if (p->parent->parent->left != NULL)
	{
		p->parent->parent->left->color = black;
	}
	if (p->parent->parent->right != NULL)
	{
		p->parent->parent->right->color = black;
	}

}

/*左旋转*/
RBTree* SingleRotateWithLeft(RBTree*& X)
{
	RBTree *P = X->parent;
	RBTree *G = P->parent;
	RBTree *U = G->right;

	RBTree* parent = G->parent;
	//查询祖父在祖父父亲的位置
	int pos = isLeft(G);
	//
	G->left = P->right;
	P->right->parent = G;
	G->parent = P;
	G->color = red;
	P->right = G;
	P->parent = parent;
	P->color = black;

	
	if (pos == 1)
	{
		parent->left = P;
	}
	else if (pos == 0)
	{
		parent->right = P;
	}
	return P;
}

/*右旋转*/
RBTree* SingleRotateWithRight(RBTree*& X)
{
	RBTree* P = X->parent;
	RBTree* G = P->parent;
	RBTree* U = G->left;
	RBTree* parent = G->parent;
	//查询祖父在祖父父亲的位置
	int pos = isLeft(G);
	G->right = P->left;
	P->left->parent = G;
	G->parent = P;
	G->color = red;
	P->color = black;
	P->left = G;
	P->parent = parent;
	
	if (pos == 1)
	{
		parent->left = P;
	}
	else if (pos == 0)
	{
		parent->right = P;
	}
	return P;
}

/*左-右双旋转*/
RBTree* DoubleRotateWithLeft(RBTree *&X)
{
	RBTree* P = X->parent;
	RBTree* G = P->parent;
	RBTree* U = G->right;
	RBTree* parent = G->parent;
	//查询祖父在祖父父亲的位置
	int pos = isLeft(G);
	P->right = X->left;
	if(X->left)
		X->left->parent = P;
	G->left = X->right;
	if(X->right)
	X->right->parent = G;
	X->left = P;
	X->right = G;
	P->parent = X;
	G->parent = X;
	X->parent = parent;
	
	if (pos==1)
	{
		parent->left = X;
	}
	else if(pos==0)
	{
		parent->right = X;
	}
	//染色
	X->color = black;
	G->color = red;

	return X;
}

/*右-左双旋转*/
RBTree* DoubleRotateWithRight(RBTree * &X)
{
	RBTree* P = X->parent;
	RBTree* G = P->parent;
	RBTree* U = G->left;
	RBTree* parent = G->parent;
	//查询祖父在祖父父亲的位置
	int pos = isLeft(G);
	G->right = X->left;
	if(X->left)
		X->left->parent = G;
	P->left = X->right;
	if(X->right)
		X->right->parent = P;
	X->left = G;
	X->right = P;
	G->parent = X;
	P->parent = X;
X->parent = parent;
	
	if (pos == 1)
	{
		parent->left = X;
	}
	else if (pos == 0)
	{
		parent->right = X;
	}
	//染色
	X->color = black;
	G->color = red;

	return X;
}

/*
调整红黑树
*/
void adjustRBTree(RBTree*& root,RBTree*& p)
{
	//父亲空指针，不需要判定
	if (p->parent == NULL)
	{
		//重新设置根节点
		root = p;
		return;
	}
	//祖父空指针，不需要判定
	if (p->parent->parent == NULL)
	{
		return;
	}
	//没有冲突，结束
	if (p->color==black||p->parent->color == black)
	{
		return;
	}
	//判断当前节点的父亲是祖父的左孩子还是右孩子
	int fPos = isLeft(p->parent);
	//红父红叔冲突
	if ((fPos==1 && (p->parent->parent->right != NULL && p->parent->parent->right->color == red))
		|| (fPos==0 && (p->parent->parent->left != NULL && p->parent->parent->left->color == red))) {
		//调整颜色即可，不需要旋转
		adjustColor(p);
		//祖宗是根节点，调整它的颜色就可以了
		if (p->parent->parent->parent == NULL)
		{
			p->parent->parent->color = black;
		}
		//将祖父节点设置为当前节点，继续调整
		else
		{
			adjustRBTree(root,p->parent->parent);
		}
	}
	//红父黑叔冲突
	else
	{
		//判断当前节点是父节点哪一个孩子
		int pos = isLeft(p);
		RBTree* result;
		//左左
		if (fPos==1&&pos==1)
	{
			result = SingleRotateWithLeft(p);
		}
		//右右
		else if (fPos==0 && pos==0)
		{
		result = SingleRotateWithRight(p);
		}
		//左右
		else if (fPos==1 && pos==0)
		{
			result = DoubleRotateWithLeft(p);
		}
		//右左
		else
		{
			result = DoubleRotateWithRight(p);
		}
adjustRBTree(root,result);
	}
}

/*
*插入节点
*/
void insert(RBTree*& root, int val)
{
	if (root == NULL)
	{
		root = new RBTree();
		root->key = val;
		root->color = black;
        	return;	}

	RBTree *t = root;
	//将要插入的节点
	RBTree *p = new RBTree();
	p->key = val;
	//先将节点插入叶子节点里
	while (true) {
		if (val > t->key)
		{
		if (t->right == NULL)
			{
				t->right = p;
				p->parent = t;
				break;
			}
			else
			{
				t = t->right;
			}
		}
		else if (val < t->key)
		{
			if (t->left == NULL)
			{
				t->left = p;
				p->parent = t;
				break;
			}
			else {
			t = t->left;
			}

		}
		else
		{
			return;
		}
	}

	//开始调整红黑树
	adjustRBTree(root,p);

}

附上cpp代码 点击下载

我们常看到的查找树都是二叉树，如二叉查找树，AVL树、伸展树等，但还有一种常用的查找树不是二叉树。这种树叫B-树，是一种多叉树。

 阶为M的B-树是一棵具有下列结构特性的树

• 树的根或者是一片树叶，或者其儿子数在2和M之间。（根可以是叶子节点，不是的话，儿子数就要在2-M之间）
  
• 除根外，所有非树叶节点的儿子树在┌M/2┐和M之间。
• 所有的树叶都在相同的深度上。

这是一棵4阶的树，可以仔细观察下。之后的插入操作都会以这棵树为demo。

应符合以下条件

• 不管什么结点，都至多有

  M  -1个关键字，

  M  棵子树（假如可以有子树的话）  ；

• 根结点如果不是叶子结点的话，那么至少有两棵子树，即至少1个关键词 ； 
• 除根以外的所有结点（包括树叶），至少有┌M/2┐-1个关键字；（┌M/2┐是取上整，└M/2┘是取下整） 
• 根据上面也不难想到  非叶子结点的关键字个数=指向儿子的指针个数-1；

有两种比较流行的B-树，一种是实际数据只存储在树叶上，还有一种是允许存储在内部节点上，如二叉查找树中所做的那样。在这里我使用的是第二种，内部节点也可以存储值。

B-树有两个比较关键的操作，插入及删除，比较麻烦。

插入的过程

    前三个节点插入比较简单，按顺序插入即可，此时根节点也是叶子节点。插入的时候先不管是否会超出m阶树的上限要求，因为定义时我们也会额外开辟一些空间。

    第四个值15，首先查找到已经有这个值了，那么便不进行插入。插入第五个值48，发现这个节点已经有4个关键字了，已经超过了要求。那么需要进行分裂。分裂操作是插入操作过程中一个最重要的操作，因为这是处理“冲突”（即结点中的数据元素大于B树规则中要求的最大个数）的一个通用的处理方式，这种方式必须要对所有的情况都适用，而分裂是解决这一问题一种方法。分裂需要父节点腾出一个key和一个child的位置，然后在需要分裂的节点里取出中间元素放进父节点腾出的key里。需要分裂的节点被一分为二，分别作为父亲的儿子。

第六个节点16插进去没有问题，下一个插入节点4，发现需要分裂。将中间元素16放进父节点。

继续插入30,17，43，插入43后需要继分裂

插,20,9无问题，25的时候需要再次分裂

42移动到父节点之后，父节点的关键字数量也超过了限制，那么父节点也需要进行一次分裂，将中间元素抽出来当做新的父节点，如下图

插入7，继续分裂

插入21，无问题，插入22，进行分裂。

分裂完之后，发现它的父节点需要继续分裂

最终所有节点插入完成。也就是这篇文章第一张图片的那棵树。

删除的过程

删除分两种情况。第一种删除的是叶子节点，如果删除之后，关键字数量还能满足要求，则结束，否则调用合并函数，合并函数是先尝试向兄弟节点借一个关键字，如果兄弟也不够了的话，就合并。
第二种是删除内部节点，找到子树中最大的一个关键字替换它（一定是叶子节点），然后对那个叶子节点执行删除，回到第一种情况。
文字不是非常理解没关系，下面上图。

这是一个5阶的B树，我们先删除0，去掉0之后，叶子节点仍然满足要求，删除结束。

我们接着删除12，我们要从这个节点的子树里找到一个关键字代替它，有两种方法，用比12小的最大关键字或比12大的最小关键字代替12(也就是前驱或者后继)，然后删掉那个儿子中的关键字，如下图。

在这两种方法里，代码实现的是第一种方式。第一种，删除11后，发现叶子节点只有一个10（图见上图中的第一种），关键字个数少于2个，此时应该合并，合并同样也有两种方式，和前一个兄弟节点合并或者后一个兄弟节点合并。

代码实现的是第一种，和前一个兄弟合并。接着我们删除9，尝试向前一个兄弟借个关键字，发现要是它借了，它也就不满足了，这时候我们就需要合并节点了，如下图。

现在我们来皮一下，直接删除根节点21。按照之前说到的，先找到比它小的最大关键字，一定在叶子节点里面，最大为20，替换根节点21后，然后删除叶子节点中的20。

发现叶子节点不满足条件了，向兄弟借一个关键字后变成下图。

接着删除17，兄弟无法帮助你，只能再次合并，结果如下。

父节点借出一个后，自己也不够了，需要对父节点再次进行合并，结果如下。

至此，删除操作的各种情况就都讲完了。在编写代码的时候，有一种特殊情况需要注意，对下面这种情况进行删除2的时候，正常合并结果如下。

因为根节点的关键字最少可以为1，所以一直没有对根进行合并，也没人能和根合并。。。遇到这种把根都删到没有关键字的时候，就需要重新设置根为原来根的第一个儿子了，代码里有体现。

代码实现

static const int m = 4;    //m阶
class BTree {
public:
	int keynum;
	int key[m + 1];				//关键字数组，多开辟一个，从1开始  0号未用， key[m]是临时空间
	BTree * parent;				//父节点指针
	BTree child[m + 1];			//孩子结点指针数组，多开辟一个  child[m]是临时空间

	//这里还涉及一个问题，如何判断一个节点是否是叶子节点，叶子节点的child[0]必定为空
	//非叶子节点的child[0]不为空
	BTree() {
		keynum = 0;
		for (int& k : key)
			k = -999;
		parent = NULL;
		for (BTree n : child) n = NULL;
	}
};

/这个结构体是查询节点返回的结果
如果，isquery是true，表明找到了这个节点，即node
如果，isquery是false，表明没有这个节点，失败于某个终端结点上，即node
如果找到了这个节点，p是在关键字中的位置，如果没有找到，返回的是应该插入的位置，例如叶子节点 1 3 5 ，寻找 4，返回的是3，方便插入。（都从1开始计数）/
struct Result {
	BTree *node;
	bool isquery;
	int p;
};

/*非递归查询节点*/
Result* findBTree(BTree* root, int k)
{
	Result* result = new Result();
	if (root == NULL)
	{
		return NULL;
	}
	BTree *r = root;
	int index = 1;
	int nowKey = r->key[index];
	while (r != NULL)
	{
		index = 1;
		while (index <= r->keynum)	//遍历所有关键字
		{
			if (r->key[index] == k)
			{
				//找到该节点
				result->isquery = true;
				result->p = index;		//该关键字在节点的位置
				result->node = r;
				return result;
			}
			if (k > r->key[index])
			{
				/*如果相等，则说明，r里面的最后一个关键字都没有k大*/
				if (index == r->keynum)
				{
					/*r已经是叶子节点了*/
					if (r->child[index] == NULL)
					{
						//没有该节点
						result->isquery = false;
						result->node = r;
						result->p = index + 1;
						return result;

					}
					/*还有儿子，遍历儿子*/
					r = r->child[index];
					break;
				}
				/*还没到最后一个关键字，继续遍历这个r*/
				index++;
				nowKey = r->key[index];
				continue;
			}
			/*比上一个大，比这一个小，应该遍历它的儿子，如果有儿子的话*/
			if (k < r->key[index])
			{
				/*是叶子节点，没儿子，无查找的节点*/
				if (r->child[index - 1] == NULL)
				{
					result->isquery = false;
					result->node = r;
					result->p = index;
					return result;
				}
				r = r->child[index - 1];
				break;
			}
		}

	}
}

/*递归查询节点*/
Result * findTree2(BTree* root, int val)
{
	Result *result = new Result;
	if (!root) {
		return NULL;
	}

	//如果比第一个关键字小，检索第一个儿子
	if (val < root->key[0] && root->child[0])
	{
		return findNode(root->child[0], val);
	}
	//如果比最后一个关键字大，检索最后一个儿子
	if (val > root->key[root->keynum - 1] && root->child[root->keynum])
	{
		return findNode(root->child[root->keynum], val);
	}
	//单独判读最后一个key
	if (val == root->key[root->keynum - 1])
	{
		result->node = root;
		result->isquery = true;
		result->p = root->keynum - 1;
		return result;
	}
	//在最边上两个关键字中间
	for (int i = 0; i < root->keynum - 1; i++) {
		if (val == root->key[i])
		{
			result->node = root;
			result->isquery = true;
			result->p = i;
			return result;
		}
		else if (val > root->key[i] && val < root->key[i + 1]) {
			return findNode(root->child[i + 1], val);
		}
	}
	//没有这个值，返回父节点，也就是某个最低层的非终端结点上
	result->node = root->parent;
	result->isquery = false;
	return result;
}

/*插入节点*/
void insertBTree(BTree* &root, int val)
{
	/*考虑B-树为空的情况*/
	if (root == NULL)
	{
		root = new BTree();
		root->key[1] = val;
		root->keynum = 1;
		return;
	}
	/*查找这个节点*/
	Result *r = findBTree(root, val);
	BTree* p = r->node;
	if (r->isquery)
	{
		//查找到了这个节点,无需插入
		return;
	}
	else
	{
		p->keynum++;				//不管怎么样，先往叶子节点里面插入
		for (int index = p->keynum; index > r->p; index--)
		{
			p->key[index] = p->key[index - 1];	//关键之往后挪一格
			p->child[index] = p->child[index - 1];	//儿子也是一样，既然叶子节点儿子都为空，那这一行就无所谓了。
		}
		p->key[r->p] = val;
		p->child[r->p] = NULL;

		/*需要分裂*/
		if (p->keynum == m)
		{
			splitBTree(p);
		}
	}
	return;
}

/*分裂*/
void splitBTree(BTree*  T)
{
	BTree* t1, *t2;
	int index, index_1;
	/*已经传递到根节点了，根也需要分裂*/
	if (T->parent == NULL)
	{
		t1 = new BTree();
		t2 = new BTree();
		t1->keynum = m / 2;
		t2->keynum = m - m / 2 - 1;
		t1->parent = T;
		t2->parent = T;

		/*初始化t1*/
		for (index = 0; index <= m / 2; index++)
		{
			t1->key[index] = T->key[index];

			/*不是叶子节点，就还需要重新分配子树*/
			if (T->child[index] != NULL)
			{
				t1->child[index] = T->child[index];
				T->child[index]->parent = t1;		//还需要更新子树的父节点
			}
		}

		/*初始化t2*/
		t2->child[0] = T->child[m / 2 + 1];
		for (index = m / 2 + 2; index <= m; index++)
		{
			t2->key[index - m / 2 - 1] = T->key[index];

			if (T->child[index] != NULL)
			{
				t2->child[index - m / 2 - 1] = T->child[index];
				T->child[index]->parent = t2;
			}

		}
		T->keynum = 1;
		T->child[0] = t1;
		T->child[1] = t2;
		T->key[1] = T->key[m / 2 + 1];
		for (index = 2; index <= m; index++)
		{
			T->child[index] = NULL;
			T->key[index] = -999;
		}
		return;
	}
	else
	{
		/*查询这个节点在父节点中的位置，（从0开始）*/
		index = whichSon(T);
		for (index_1 = T->parent->keynum; index_1 > index; index_1--)
		{
			T->parent->key[index_1 + 1] = T->parent->key[index_1];
			T->parent->child[index_1 + 1] = T->parent->child[index_1];
		}
		T->parent->keynum++;
		T->parent->key[index + 1] = T->key[m / 2 + 1];
		/*t2为新的节点*/
		t2 = T->parent->child[index + 1] = new BTree();
		t2->keynum = m - (m / 2 + 1);
		t2->parent = T->parent;
		/*因为没有key[0]，所以要单独初始化child[0]，不用for一起初始化*/
		t2->child[0] = T->child[m / 2 + 1];
		/*初始化t2*/
		for (index = m / 2 + 2; index <= m; index++)
		{
			t2->child[index - m / 2 - 1] = T->child[index];
			t2->key[index - m / 2 - 1] = T->key[index];
		}

		T->keynum = m / 2;
		for (index = (m / 2) + 1; index <= m; ++index)  //初始化T
		{
			T->child[index] = NULL;
			T->key[index] = -999;
		}
		/*父亲也需要分裂，递归*/
		if (T->parent->keynum == m)
		{
			splitBTree(T->parent);
		}
		return;
	}
	
}

/*查询T是父节点的第几个孩子(从0开始计数)  失败返回-1*/
int whichSon(BTree* T)
{
	int index = -1;
	if (T == NULL)
		return -1;
	for (index = 0; index <= T->parent->keynum; index++)
	{
		if (T == T->parent->child[index])
			return index;
	}
	return -1;
}

/*寻找当前节点所有儿子中最大的关键字*/
Result* findMax(BTree* T)
{
	if (T == NULL) return NULL;
	BTree *p = T;
	while (p->child[p->keynum] != NULL)
		p = p->child[p->keynum];
	Result *r = new Result();
	r->isquery = true;
	r->node = p;
	r->p = p->keynum;
	return r;
}

void borrowBNode(BTree* &root, BTree *T)
{
	int mynum, bronum, index;
	BTree* b;
	BTree* f = T->parent;
	/*考虑父节点不存在的情况，理论上是不会出现这种情况*/
	if (f == NULL)
	{											
		return;
	}
	/*找到当前节点是父节点的第几个儿子（从0开始 */
	mynum = whichSon(T);
	if (mynum == 0)
		bronum = 1;
	else
		bronum = mynum - 1;
	b = f->child[bronum];

	/*如果兄弟帮不了你，即它给你一个关键字，它就不满足条件了*/
	if (b->keynum == (m + 1) / 2 - 1)
	{
		/*和兄弟合并*/
		/*如果我是第一个节点*/
		if (bronum > mynum)
		{
			/*交换T和b的值，再进行合并，保证b是T父节点的前一个儿子*/
			BTree *tmp = T;
			T = b;
			b = tmp;
			int tmpp = bronum;
			bronum = mynum;
			mynum = tmpp;
		}

		/*现在b一定是在T前面，T合并到b里*/
		b->keynum++;
		b->key[b->keynum] = f->key[mynum];
		b->child[b->keynum] = T->child[0];
		for (index = 1; index <= T->keynum; index++)
		{
			b->keynum++;     
			b->key[b->keynum] = T->key[index];
			b->child[b->keynum] = T->child[index];
		}
		/*调整父节点*/
		for (index = mynum; index <= f->keynum; index++)
		{
			f->key[index] = f->key[index + 1];
			f->child[index] = f->child[index + 1];
		}
		f->keynum--;
		f->key[0] = -999;
		/*父节点不是根节点，且不满足条件，也需要调用合并函数*/
		if (f->keynum <= (m + 1) / 2 - 2 && f->parent != NULL)
		{
			borrowBNode(root, f);
		}
		/*根节点已经删的没有关键字了，重新设置根节点*/
		if (root->keynum == 0)
		{
			if (root->child[0] != NULL)
				root = root->child[0];
		}
	}
	/*如果兄弟可以帮你*/
	else
	{
		/*如果我是第一个节点*/
		if (bronum > mynum)
		{
			T->keynum++;
			T->key[T->keynum] = f->key[bronum];
			T->child[T->keynum] = b->child[0];
			f->key[bronum] = b->key[1];
			b->child[0] = b->child[1];
			for (index = 1; index <= b->keynum; index++)
			{
				b->child[index] = b->child[index + 1];
				b->key[index] = b->key[index + 1];
			}
			b->keynum--;
		}
		/*如果我不是第一个节点*/
		else
		{
			T->child[1] = T->child[0];
			for (index = 1; index <= T->keynum; index++)
			{
				T->key[index + 1] = T->key[index];
				T->child[index + 1] = T->child[index];
			}
			T->child[0] = b->child[b->keynum];
			T->key[1] = f->key[mynum];
			f->key[mynum] = b->key[b->keynum];
			T->keynum++;
			b->child[b->keynum] = NULL;
			b->key[b->keynum] = -999;
			b->keynum--;

		}

	}
}

/*删除节点*/
void deleteBTree(BTree* &root, int val)
{
	int index;
	if (root == NULL)
		return ;
	Result* r = findBTree(root, val);
	/*没查询到这个节点*/
	if (!r->isquery)
		return ;
	BTree* p = r->node;
	/*如果是叶子节点*/
	if (r->node->child[0] == NULL)
	{
		for (index = r->p; index <= p->keynum; index++)
		{
			p->key[index] = p->key[index + 1];
		}
		p->key[p->keynum] = -999;
		p->keynum--;
		/*叶子节点关键字数量不够。既是树叶同时又是根的话就不需要合并了，只需要关键字数大于1就行了*/
		if (p->keynum <= (m + 1) / 2 - 2 && p->parent != NULL)
		{
			/*借兄弟节点*/
			borrowBNode(root, p);
		}
		return ;
	}
	/*如果是内部节点*/
	else
	{
		/*找到儿子里的最大节点，替换要删除的节点*/
		Result *re = findMax(p->child[r->p - 1]);
		BTree *q = re->node;
		p->key[r->p] = q->key[re->p];
		q->key[re->p] = -999;
		q->keynum--;
		/*如果叶子节点关键字数量不够*/
		if (q->keynum <= (m + 1) / 2 - 2)
		{
			/*借兄弟节点*/
			borrowBNode(root, q);
		}
		return ;
	}
}

        在写首页的展示文章功能的时候，当然是少不了分页的。文章需要展示标签，一篇文章可能有多个标签，是一对多的关系。某一篇文章有四条数据，如图

        测试一页展示两篇文章的时候，惊奇的发现，那一页只显示了一篇文章"使用正则获取..."，而且四个标签只显示了两个，再看下上面查询的结果，似乎明白了，下一页是同样也是只有一篇文章，标签是剩下的两个。

        因为一篇文章有多个标签，所以limit不能写死，如下，要不然谁知道你一页会有几篇文章呢，反正一页的标签数是肯定一样的了。

select
    a.*,t.*
    from article a,tag t,article_tag a_t 
    where a.articleId=a_t.articleId and t.tagId=a_t.tagId
    order by pubdate desc
    limit 5,2

        这时候想到的办法是是limit需要一个公式，动态的来分页，上面语句里的5和2都应该是动态变化的，比如一页十篇文章。但问题也随之而来，我如何知道第一页应该是哪十个？这个可以根据group by (articleId) 来保证一篇文章只显示一次，但又该如何知道一篇文章有几个标签，用count?那一篇文章就要查一次，效率实在低下，这个思路就先放一放了。

        那我们就一次查询完所有文章，然后前台分批次去取数据，但想一下，如果上万条文章怎么办，这一次查询要多久....而且查了那么多数据，我根本看不到那里，白查!不可取。

        那我只能先查文章主表，查出十条记录，然后在到关系表中查到相关的标签，一条文章就要查询一次标签。效率也比较低下。项目跑起来效果的确是这样，刷新一次需要等待肉眼可见的时间，体验很差。。。但就先凑活着，我相信这绝对不是好方案，sql会有相关的知识，而我不知道罢了。

        果然两三天后，一不小心浏览到group_concat，能将多行数据整合到一行上面，配合group by 的话，这不就是我想要的吗？立刻尝试编写sql语句

select   
    a.*,group_concat(t.tagName)
    from article a,tag t,article_tag a_t
    where a.articleId=a_t.articleId and t.tagId=a_t.tagId
    group by articleId
    order by pubdate desc

        视图多了一个长文本字段，查看一下，会发现已经把所有想要的添加进来了，并且默认使用逗号进行分割，总算找到你了，知识的广度很重要。

        下面就只要修改下mapper的XML文件，大功告成了。刷新下主页，获取文章的速度明显变快。

  <resultMap id="ArticleTagMap2" type="net.peihuan.entity.Article" extends="ResultMapWithBLOBs">
    <result column="group_concat(t.tagName)" property="grouptags" jdbcType="LONGVARCHAR" />
  </resultMap>
  <!-- 查询所有文章基本信息及他们的标签 -->
  <select id="selectAllArticlesWithTags" parameterType="map" resultMap="ArticleTagMap2">
    select
    a.*,group_concat(t.tagName) from
    article a,tag t,article_tag a_t
    where a.articleId=a_t.articleId
    and t.tagId=a_t.tagId
    group by articleId
    order by pubdate desc
    limit #{beginIndex},#{offset}
  </select>

        发现mybatics自带分页功能，可以了解一下。

我的博客

        我想绝大多数写代码的都想有一个属于自己的域名，属于自己的网站，我也一样，只不过一直没有机会实现。但自从某日浏览了一个博客，嗯，这也太好看了吧？怎么做的？教练，我想学这个...恰巧这段时间刚好在学web开发，天时地利人和。

        看了下喜欢的那个博客，down下来是hexo的主题，看着一堆没见过的后缀名，和屏幕对脸懵逼，啥玩意啊，不会用。不会前端，只会简单改改html文件，于是便使用wget命令直接把整个网站拿了下来变成了静态的。前台剩下也就没什么了。

        后台使用的java开发，IDE用的idea，稍微有点jsp、servlet的底子，会写个简单的注册登录。但想用框架，花了一天时间按网上的教程搭了个ssm框架，写了个简单的demo，算是完成了。剩下的无非就是对数据库的增删改查了，富文本编辑器一开始用的百度的，但一直乱码，百度貌似也不维护了，最后换了wangeditor，非常轻量简洁，很喜欢。

        功能基本完成的差不多之后，觉得URL里面是jsp非常丑，其实前台全部使用的ajax异步获取的数据，遂全部将后缀改成html。还有一些小问题还需要慢慢解决！如有人发现了一些bug，请告知我，不胜感激。

个人

        95后，即将毕业于某小县城末流二本。

        不抽烟、不喝酒、不近女色（假的）、

        喜欢技术，热衷于制造bug！

        喜欢唱歌，可惜五音不全、喜欢跳舞，可惜肢体不协调、

        喜欢画画，又奈何是个灵魂画手、

        喜欢吹笛子，奈何连声都吹不响、

        喜欢虾jb逛，不对，喜欢旅游，但是又穷、

        能玩的起来的也就是睡睡觉、打打王者了

        攒钱，有很多想去的地方、

        搞艺术是不可能搞艺术的了，这辈子都搞不起来了，超级羡慕会唱歌跳舞画画之类的，现在只能靠搬搬代码这样子才
        能维持得了生活，github里面的老哥个个都是人才，说话又好听，我超喜欢这里的。

在搭建这个博客的时候，前台一开始都使用的jsp，使用了很多<% %>，比较难看，可读性也较差，后来逐渐全部换成了ajax获取数据，这时候觉得已经没必要使用jsp了。

使用jsp后缀也导致URL链接也非常丑（个人感觉），遂把所有jsp后缀改成html。刷新页面发现报错，

<%request.getParameter("xxx")%>

因为不是jsp，所以这种方法也行不通了。
但js里面有一个方法可以获取页面的URL地址

window.location 对象所包含的属性

window.location.search 来获取?之后的所有参数。

window.location.search.substr(1)

使用substr(1)来去掉 ? 

reg = new RegExp("(^|&)" + name + "=([^&])(&|$)", "i");

使用正则，如下图，i表示忽略大小写

var r = window.location.search.substr(1).match(reg);

匹配之后会的r为一个数组，长度为4。第一个是整个匹配的字符串，第二个是group1，第三个是group2,第四个是group3。因为使用了捕获，如果不行使用捕获的话括号里面加个?:就可以了。如(?:^|&)。

那么r[2]就是我们想要的参数，完整函数如下

function getQueryString(name) {
    var reg = new RegExp("(^|&)" + name + "=([^&])(&|$)", "i");
    var r = window.location.search.substr(1).match(reg);
    if (r != null) return decodeURI(r[2]); return null;
}

复习一下平衡二叉树，经常混以为就是最优二叉树，其实是最优二叉树是哈夫曼树，这个以后有机会再说。

平衡二叉搜索树（Self-balancing binary search tree）又被称为AVL树（有别于AVL算法），且具有以下性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树,它须保证树的深度是O(log N)。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 最小二叉平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列，可以参考Fibonacci(斐波那契)数列，1是根节点，F(n-1)是左子树的节点数量，F(n-2)是右子树的节点数量。

  这里主要思考的是二叉树的插入节点。查询节点和修改节点的操作都可以以时间O(logN)的复杂度执行，假如删除使用惰删除的话，那么时间也是O(logN)。所谓惰删除就是当删除一个节点时，并不是真正的进行了物理删除，只是设置了一个字段来标记这个节点是否被删除。使用惰删除是有很多好处的，物理删除可能将会像插入节点一样需要进行旋转，当然也可能不需要。但如过后期又想添加之前删除的节点，那么又只能重新插入节点，很大几率要进行旋转操作。如果使用惰删除，那么时间复杂度将大大降低，但是相应的会使用额外的存储空间。

  如果插入一个节点将导致一个树的不平衡，那么会有一个必须重新平衡的节点叫做α。由于任意节点最多有两个孩子，因此高度不平衡时，α两棵子树的高度差为2，这种不平衡可能会出现以下四种情况：

1.对α的左儿子的左子树进行一次插入。
2.对α的左儿子的右子树进行一次插入。
3.对α的右儿子的左子树进行一次插入。
4.对α的右儿子的右子树进行一次插入。

  情况1和4是对称的，情况2和3是对称的，所以实际上只有两种情况，但是编程还是要写四种情况。
  情况1和4是插入发生在“外边”的情况，左-左，右-右，这种情况通过一次单选转就可以完成调整，剩下两种情况是插入发生在“内部”的情况，左-右，右-左，这种情况需要进行双旋转来进行调整。

插入原理

单旋转

  上图是左单旋转，对k2的左儿子k1的左子树进行的一次插入，X、Y、Z分别表示表示k1、k2的儿子，可以看见X明显比Y和Z深，且比Z深2层。为恢复平衡，就应该把X上移一层，Z下移一层，这样就变成了上图中旋转后的样子，k2变成了k1的右孩子，Y变成了k2的左孩子，X和Z不变。

  右旋转类似，对k1的右孩子k2的右孩子进行了一次插入，导致Z的深度比X大2，同样是把X下移一层，Z上移一层，k1就变成了k2的左孩子，Y变成了k1的右孩子。

  个人是这样记忆的，如何找到哪个是k1哪个是k2呢？k1和k2必定有一个是不平衡的，先找到这两个节点，然后不管是左还是右旋转，都让k1小于k2，也就是大的节点是k2，小的节点是k1，k1、k2互换高度，一个上移，一个下移。

双旋转

但是单旋转无法解决另外两种情况

  我们要把Y看成是一个根和两棵子树，B和C中有一个比D深两层（除非它们都是空的），我们不能确定是哪一棵，也不需要确定是哪一棵，上图中画的时候B和C全部画的比D低一层半。整颗子树，我们看成四棵子树A、B、C、D和三个节点！k1、k2、k3。
  为了重新平衡，我们不能让k3继续当根节点，k1页不行，唯一的选择就是k2当做新的根。k1、k3分别作为k2的左右孩子，巧妙的是，A、B、C、D四棵子树依旧是按顺序排列过去的。

右-左双旋转如上，基本差不多。

总结下，遇到双旋转，先找到k1、k2、k3，三个节点最小的是k1，最大的是k2，旋转后，k1是k2左孩子，k3是k2右孩子，A、B、C、D依旧是原顺序排列。

对于插入，最多只需要一次旋转（如果双旋转也只视作一次旋转）

删除原理

AVL树的删除和BST的删除较为类似，首先找到需要删除的节点，找到之后，分为三种情况进行删除。

• 需要删除的节点D是叶子节点，这种情况最简单，删除D之后，判断父节点DP是否需要调整，调整完成之后再调整DPP，DPPP，直到回溯到根节点。
• 需要删除的节点D有一个孩子，将D的值改为孩子的值，然后删除叶子节点，这样就把情况转换成第一种情况了。
• 需要删除的节点D有两个孩子，将D的值改为前驱或者后继的值，然后删除前驱或者后继的值，这样也就把情况装换成第一种情况了。

由此可见，我们只要重点讨论第一种情况就可以了，具体的删除流程如下：

1. 删除节点D
2. 判断删除节点的父节点DP是否满足AVL树的性质，如果不满足，则根据DP的状态进行旋转调整，并重新计算DP的高度，旋转分为四种情况，这里就不再细说。
3. 继续向上调整DPP，检查DPP的平衡是否遭到破坏，之后再继续向上调整DPP，直到调整到根节点为止（即不断执行第三步）。实际上这里可以进行优化，在调整过程中如果经过某一次的调整，树的高度没有发生变化，那么就不必向上回溯调整了。

如何判断是否需要向上回溯调整呢？根据平衡因子。
  如果删除一个节点后，平衡因子为1/-1，说明高度未发生变化，那么就不需要向上调整了；如果删除一个节点后，因子变成0，说明树高度一定发生了变化，那么就需要向上回溯调整。如果平衡因子为2/-2，说明需要调整这棵树需要调整。

这里可以看到AVL树的可视化。

代码实现

  将一个新节点，插入到AVL树中去，递归的插入到相应的子树中后，如果树的高度不变，那么插入完成，如果出现了高度不平衡，那么我们将做适当的双旋转或者单旋转，并更新这些高度。另外一个问题就是二叉树的高度信息的存储，由于真正需要的是实际是子树高度的差，并且它一般很小，（1,0，-1等）

java的完整实现 点这里

下面给出的是C的代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class AvlNode {
public:
    AvlNode *left;
    AvlNode *right;
    int val;
    int height;        //这个节点的高度

    AvlNode() {
        left = NULL;
        right = NULL;
        val = -9999;
        height = 0;
    }
    AvlNode(int v) {
        left = NULL;
        right = NULL;
        val = v;
        height = 0;
    }

};

1
2
3
4
5
6
7
8

/*返回某个节点的高度*/
static int Height(AvlNode* node)
{
    if (node == NULL)
        return 0;
    else
        return node->height;
}

1
2
3
4
5
6
7
8
9
10
11
12

/*左单旋转*/
static AvlNode* SingleRotateWithLeft(AvlNode *k2)
{
    AvlNode *k1 = k2->left;
    k2->left = k1->right;
    k1->right = k2;

    k2->height = max(Height(k2->left), Height(k2->right)) + 1;
    k1->height = max(Height(k1->left), k2->height) + 1;

    return k1;
}

1
2
3
4
5
6
7
8
9
10
11
12

/*右单旋转*/
static AvlNode* SingleRotateWithRight(AvlNode *k1)
{
    AvlNode *k2 = k1->right;
    k1->right = k2->left;
    k2->left = k1;

    k1->height = max(Height(k1->left), Height(k1->right)) + 1;
    k2->height = max(k1->height, Height(k2->right)) + 1;

    return k2;
}

1
2
3
4
5
6
7
8
9

/*左-右双旋转*/
static AvlNode* DoubleRotateWithLeft(AvlNode *k3)
{
    /*k1,k2先右单旋转*/
    k3->left = SingleRotateWithRight(k3->left);

    /*k3,k2再左单旋转*/
    return SingleRotateWithLeft(k3);
}

1
2
3
4
5
6
7
8
9

/*右-左双旋转*/
static AvlNode* DoubleRotateWithRight(AvlNode *k1)
{
    /*k3,k2先左单旋转*/
    k1->right= SingleRotateWithLeft(k1->right);

    /*k1,k2再右单旋转*/
    return SingleRotateWithRight(k1);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

/*
向AVL树种插入节点
*/
AvlNode* insert(int val, AvlNode *T)
{
    if (T == NULL)
    {
        T = new AvlNode(val);
    }
    /*向左孩子插入*/
    else if (val < T->val)
    {
        T->left = insert(val, T->left);
        if (Height(T->left) - Height(T->right) == 2)
        {
            if (val < T->left->val)
                T = SingleRotateWithLeft(T);
            else
                T = DoubleRotateWithLeft(T);

        }
    }
    /*向右孩子插入*/
    else if (val > T->val)
    {
        T->right = insert(val, T->right);
        if (Height(T->right) - Height(T->left) == 2)
        {
            if (val > T->right->val)
                T = SingleRotateWithRight(T);
            else
                T = DoubleRotateWithRight(T);
        }
    }

    /*计算这个节点新的高度*/
    T->height = max(Height(T->left), Height(T->right)) + 1;
    return T;

}

在想如何获取文章摘要的时候，有若干个想法，
第一，在获取到文章后，直接截取前100个字符，但因为是富文本，存在数据库时有很多html标签，如果前一百个截断了html怎么办？或者去掉所有html标签再截取，但就失去了文本格式；
第二，在数据库中文章表中添加一个摘要字段，如果写文章时候不修改，那么就默认为第一段或者前多少个字，当然也可以手动修改，但是非常不想用这样方法。

之后，在网上看到别人想法，使用第一个<p></p>标签中的文字作为摘要。而且正常第一段文字的确是大部分技术类博客的主要内容。

第一想法就是使用正则，来找到第一个<p>,但是<p>里面可能会有张<img> 这不是我们想要的摘要，所以我们需要过滤掉<img>，边学边用正则，起初脑子里一直盯着^这个字符（取反），比如这样^(<img)，或者(^<img)，当然都是不对的，应当使用前瞻，我要匹配<p>且下一个字符不是<img>的，中间任意，最后以</p>结尾.

(?=exp) 匹配exp前面的位置
(?<=exp) 匹配exp后面的位置
(?!exp) 匹配后面跟的不是exp的位置
(?<!exp) 匹配前面不是exp的位置

直接给出代码

private String getDigest(String content){
        //正则筛选第一个文字<p>
        Pattern datePattern = Pattern.compile("<p>((?!<img).)*?<\\/p>");
        Matcher dateMatcher = datePattern.matcher(content);
        if(dateMatcher.find()) {
            return dateMatcher.group();   //返回第一个<p>
        }else
        {
            return "null";
        }
    }